だいぞう
だいぞう
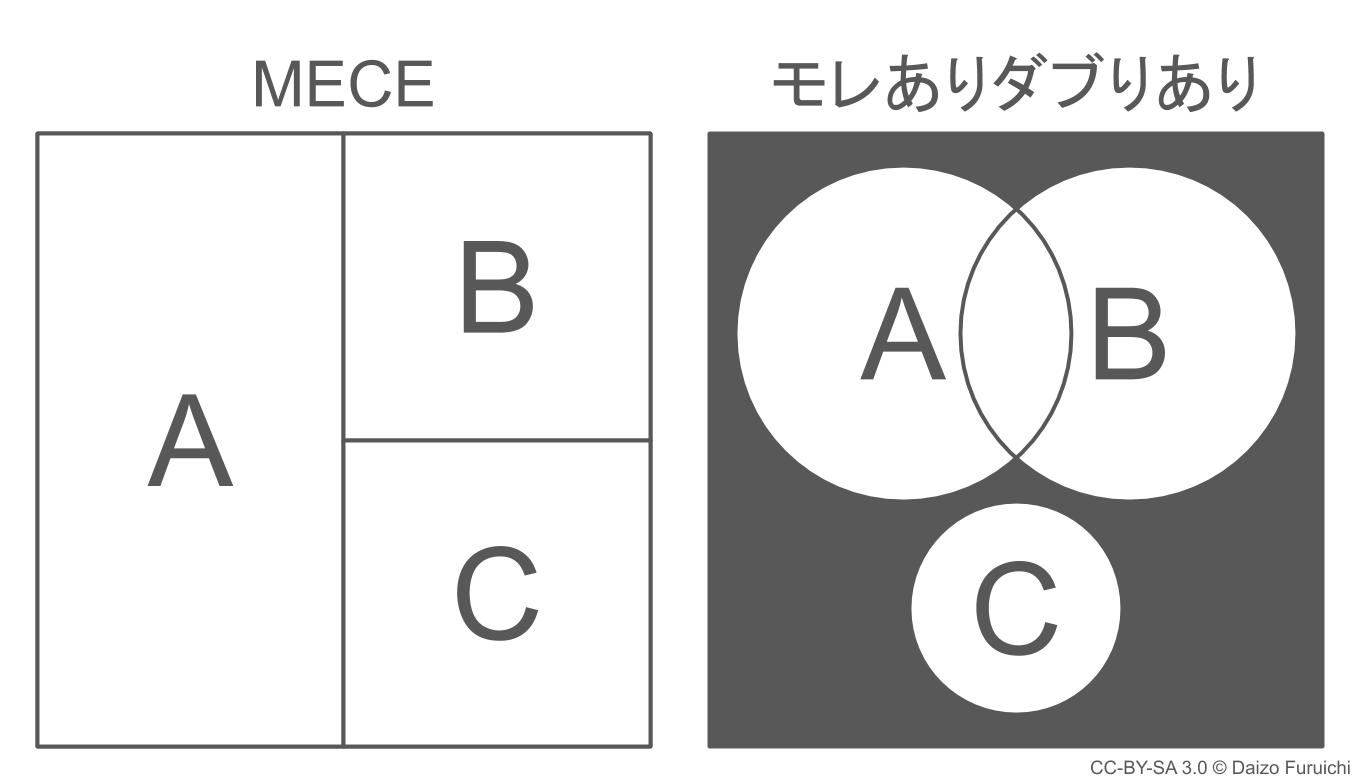
MECEとは、
- モレなくダブりなく
という意味の英語「Mutually Exclusive and Collectively Exhaustive」の頭文字を取ったものです。
読み方は「ミーシー」が一般的で、ロジカル・シンキング(論理的思考)やアイデアの切り口として、経営者やコンサルタントに必要とされる基礎的な情報整理の技術とされています。もちろん、社会人として身につけておけば、色々な場面で役立ちます。
MECEの状態を図で表すと、下図のようになります。
このモレなくダブりない状態を実現するグループ化の方法は、
- 因果関係によるグループ化
- 類似性によるグループ化
- 構造によるグループ化
の3つに分類することができます。
さらに3つ目の「構造によるグループ化」は、
- 二項対立
- 分割
- 尺度
- プロセス
- 因数分解
の5つのタイプに分けることができます。
ここでは、MECE(モレなくダブりなく)について、わかりやすく説明します。
MECE(ミーシー)はロジカルシンキングの基本
MECE(ミーシー)とは、経営者やコンサルタントに求められる、情報を整理するための基礎的なテクニックのことです。
ロジカルシンキング(論理的思考)とは切っても切り離せない手法で、情報をわかりやすく分類し、順序立てて説明する時に役立ちます。
1970年代にMECEという考え方を発案したのは、世界的なコンサルティング会社「マッキンゼー社(McKinsey & Company)」のバーバラ・ミント氏です。
ミント氏は著書でMECEを、
- 個々に見て「ダブリ」がなく(Mutually Exclusive)
- 全体的に見て「モレ」がない(Collectively Exhaustive)
バーバラ・ミント著「新版 考える技術・書く技術 」第6章 p115 より引用
というように説明をしています。
この著書「新版 考える技術・書く技術(原題:The Minto Pyramid Principle、ミントのピラミッド原則)」の中で、
- ピラミッドの構造によるグループ化
を行う場面で「MECE」が登場します。
3つのグループ化によるMECE(ミーシー)
先ほどのピラミッド原則を満たすようなグループ化の方法としては、
- 因果関係によるグループ化
- 類似性によるグループ化
- 構造によるグループ化
の3つの方法があるとされています。
「MECE」という考え方は、この3つのうちの「構造によるグループ化」のコツとして説明されています。
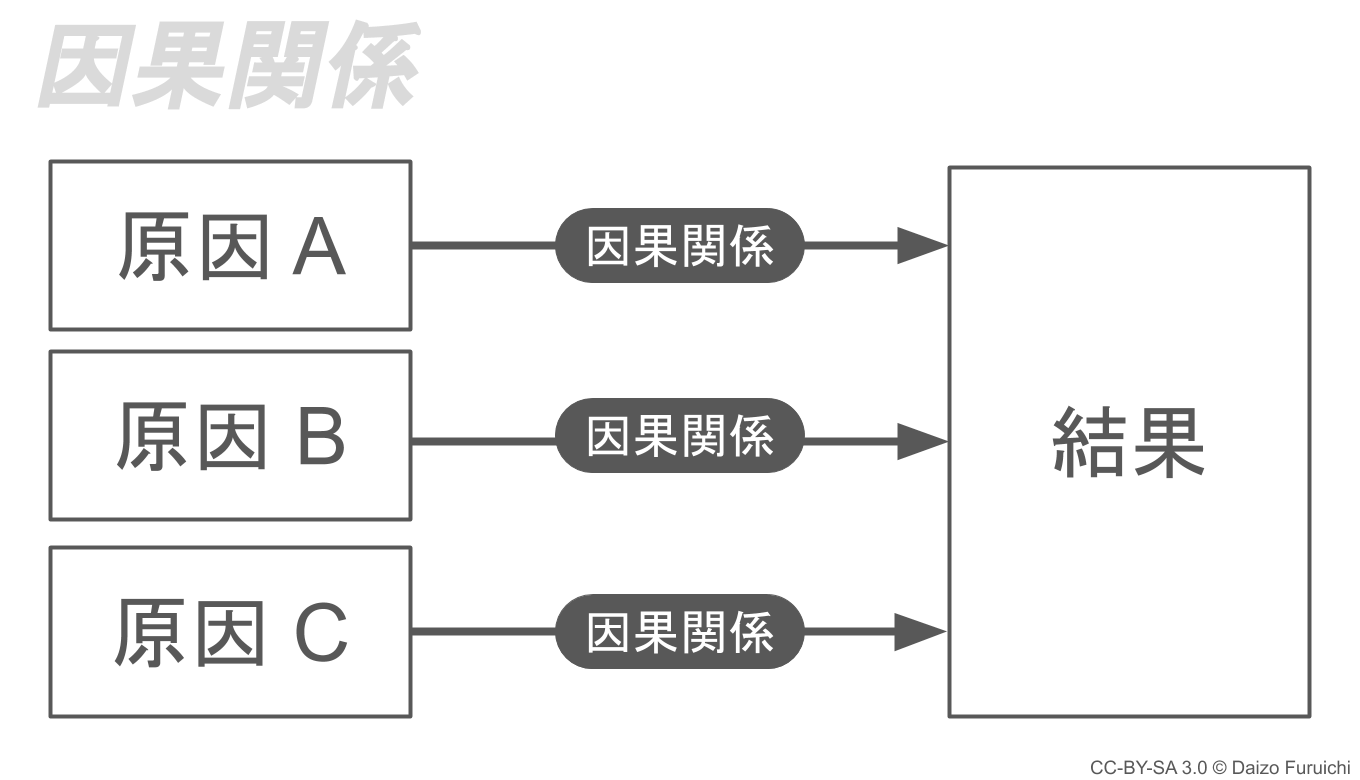
ちなみに「因果関係」と「類似性」のグループ化でMECEが語られないのは、
- 因果関係
- 全ての原因を挙げることができればモレがない
- 原因を個々のレベルに分解できればダブらない
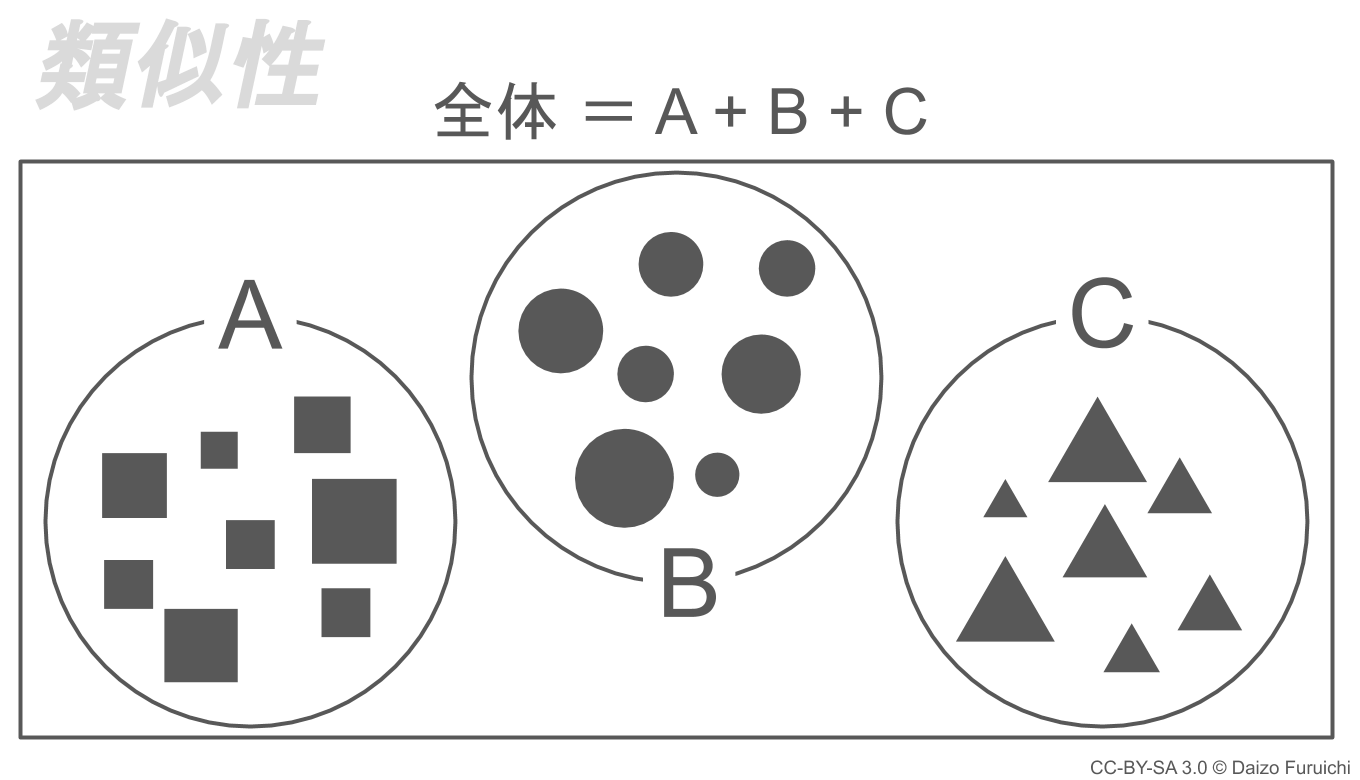
- 類似性
- そこにあるものが全てと定義すればモレがない
- それぞれの特徴を具体的に定義できればダブらない
という理由です。
因果関係によるグループ化のイメージは、下図のようになります。
そして類似性によるグループ化のイメージは、下図のようになります。
どちらのグループ化も、ぱっと見でモレなくダブりないMECEの状態になっていることがわかると思います。
つまり材料さえきちんと揃っていれば、「因果関係」と「類似性」は自然とMECEの状態になりやすい方法なのです。(だからといって、モレやダブりが発生しないわけではありません。)
余談ですがMECEの説明として、
- トップダウン型アプローチ
- ボトムアップ型アプローチ
を挙げている方もいらっしゃいます。しかし、この2つのアプローチは「ピラミッド構造の作り方」であって、「MECEのやり方」ではありません。バーバラ・ミント著「新版 考える技術・書く技術 」では、
- 第1章 なぜピラミッド構造なのか?
- 第3章 ピラミッド構造はどうやって作るのか?
に、トップダウンとボトムアップの説明が登場しています。そしてMECEが登場するのは第6章以降です。
ここまでの話を整理すると、
- 情報を整理するためのピラミッド構造がある
- ピラミッド構造の要点はグループ化にある
- グループ化の方法は「因果関係」「類似性」「構造」の3つがある
- 「因果関係」「類似性」は自然とMECEになりやすい
- 「構造」はMECEを意識しないとモレやダブりが生まれやすい
ということです。