だいぞう
だいぞう
ロジカルシンキング(Logical thinking、論理的思考)とは、
- 情報を分解し再構成して筋の通った結論を導く考え方
のことです。
一方で、似た言葉として挙げられる「クリティカルシンキング(Critical thinking、批判的思考)」とは、
- 情報を観察し分析することで結論を検証する
ことです。
つまり、この2つの考え方をよりシンプルに表現すると、
- ロジカル・シンキング:筋の通った結論を生み出すこと
- クリティカル・シンキング:結論に筋が通ってるか疑うこと
という相反する性質を持っていることがわかります。
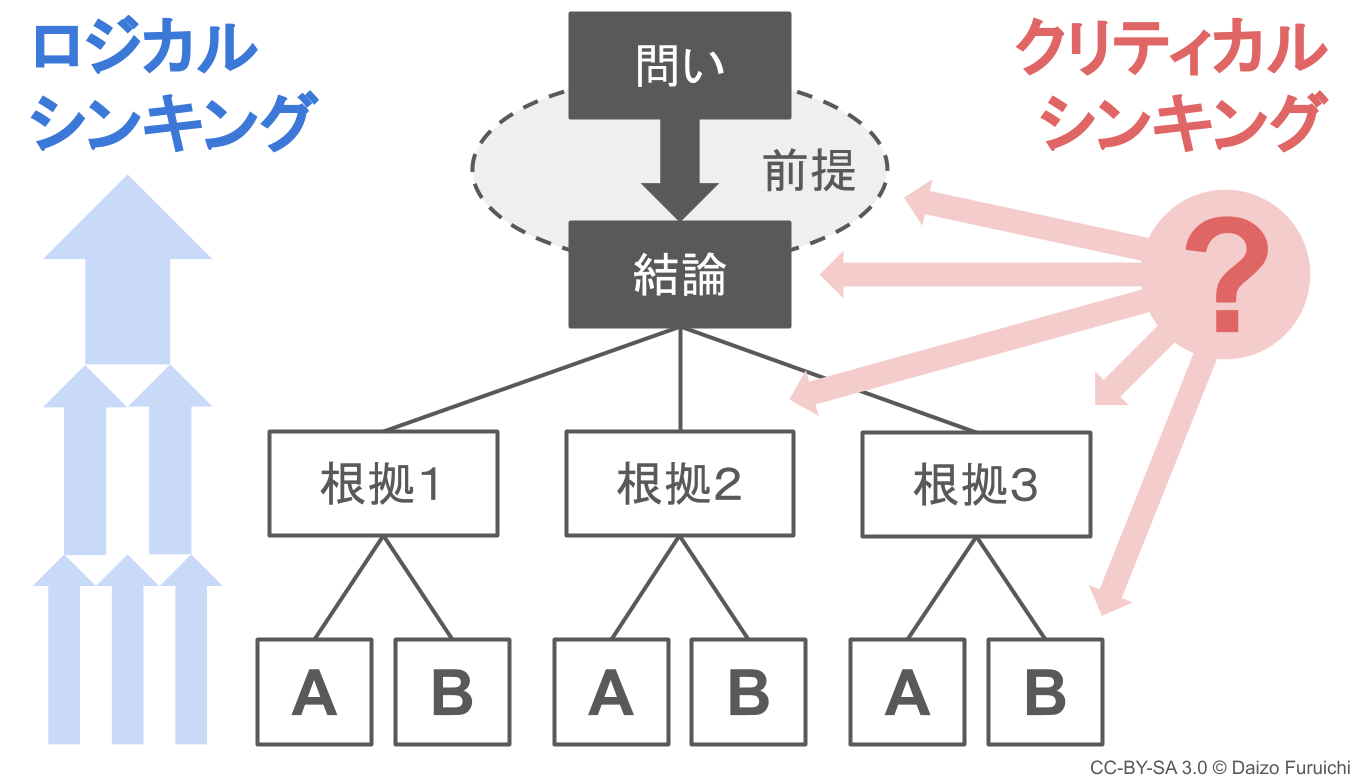
ここでは、ロジカルシンキング(論理的思考)を中心に、クリティカルシンキング(批判的思考)との関係性と併せて、思考の鍛え方をわかりやすく図解します。
ロジカルシンキングとは?
ロジカルシンキングとは、その名の通り論理的(情報が理路整然とした)な思考法のことです。
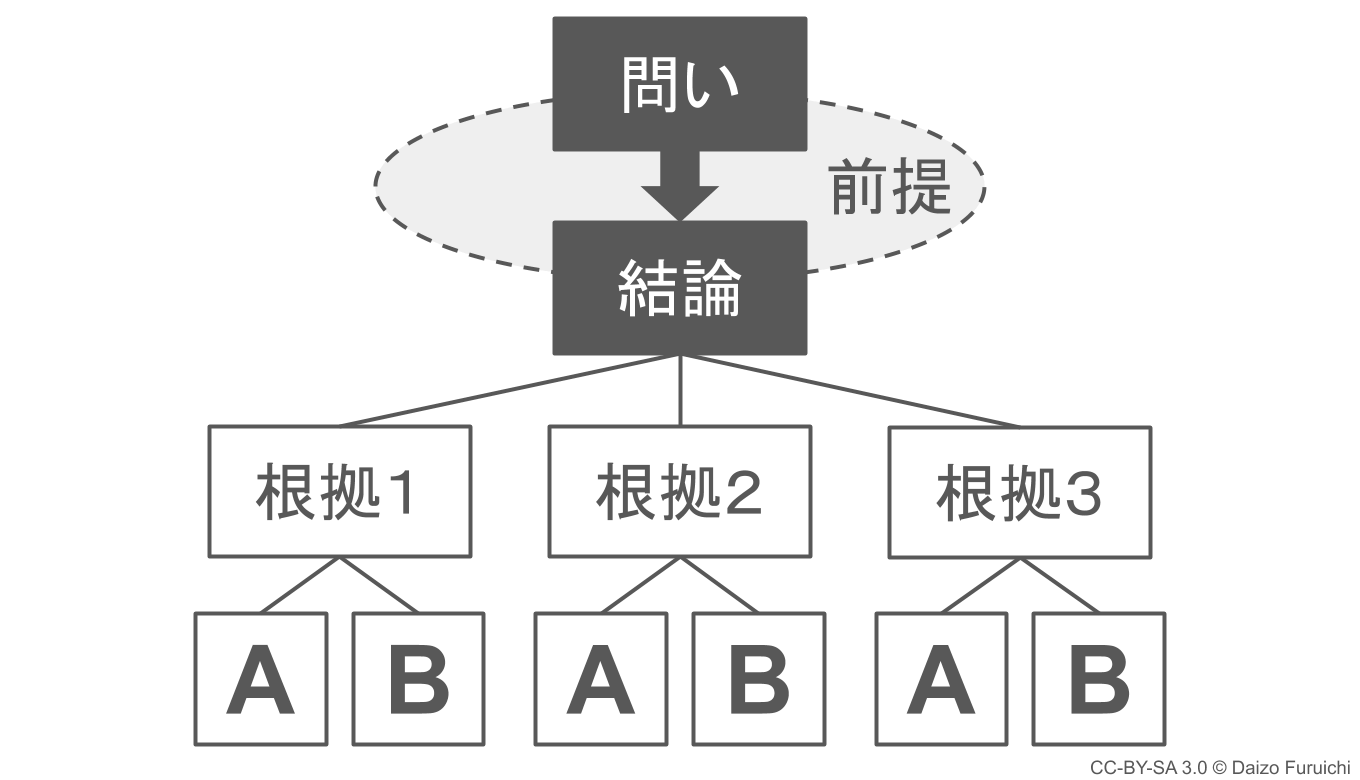
ロジカルシンキング(論理的思考)では、
- 状況を取り巻く前提
- 様々な情報
をもとに、
- 正しい「問い」
を設定し、根拠に基づいた結論を導きます。
例えば、
- 前提:不採算店舗は閉鎖する会社の方針
- 情報:店舗Aは直近一年の利益が赤字
という状況であれば、
- 問い:店舗Aは閉鎖するべきか?
- 結論:店舗Aは閉鎖するべきだ。
- 根拠:店舗Aは不採算店舗の撤退条件を満たしている
と考えることができるかもしれません。これをまとめると「店舗Aは直近一年の利益が赤字であり、不採算店舗の撤退条件を満たしている。だから店舗Aは閉鎖するべきだ。」という筋の通った結論を主張することができます。
そのためには、
- 様々な情報を集めて分解し
- 正しい問いを見つけて掘り下げ
- 根拠を組み立て
- 結論を導く
といったロジカルシンキングの一連の作業が必要になります。
この一連の作業をスムーズに行うためには、
- 因果関係や相関関係
- 仮説推論(演繹法、帰納法、アナロジー、アブダクション)
といった思考テクニックや、
- ピラミッドストラクチャー:情報を整理するためのピラミッド構造
- ロジックツリー:問題解決に特化したピラミッドストラクチャー
- MECE(ミーシー):モレなくダブりなく情報を分類する手法
といったフレームワークが使われています。これらについては、後ほど詳しく説明します。
正しい「問い」の重要性
ロジカルシンキングでは、正しい「問い」を立てることが「筋の通った結論」を導くことと同じくらい重要です。
なぜなら「問い」によって「結論」が大きく変わるからです。
先ほどの例で言えば、
- 問い:店舗Aは閉鎖するべきか?
- 結論:店舗Aは閉鎖するべきだ。
という形でお互いに対応しています。
しかし、
- 問い:店舗Aの店長を変えるべきか?
だったり、
- 問い:店舗Aの赤字を補填し続けるべきか?
だったりすれば、それぞれの結論は大きく違うものになるはずです。
つまり、いくらロジカルシンキングで筋の通った結論を導いたとしても、問いそのものが間違っていると無意味な結論になってしまいます。
そのためには、次に説明する「クリティカルシンキング」を使って、
- 導こうとしている結論に対する問いそのものが正しいのか?
ということを考えなければいけません。
次のページからは、論理的思考を補い、鍛え上げる役割を果たす「クリティカルシンキング(批判的思考)」について説明します。