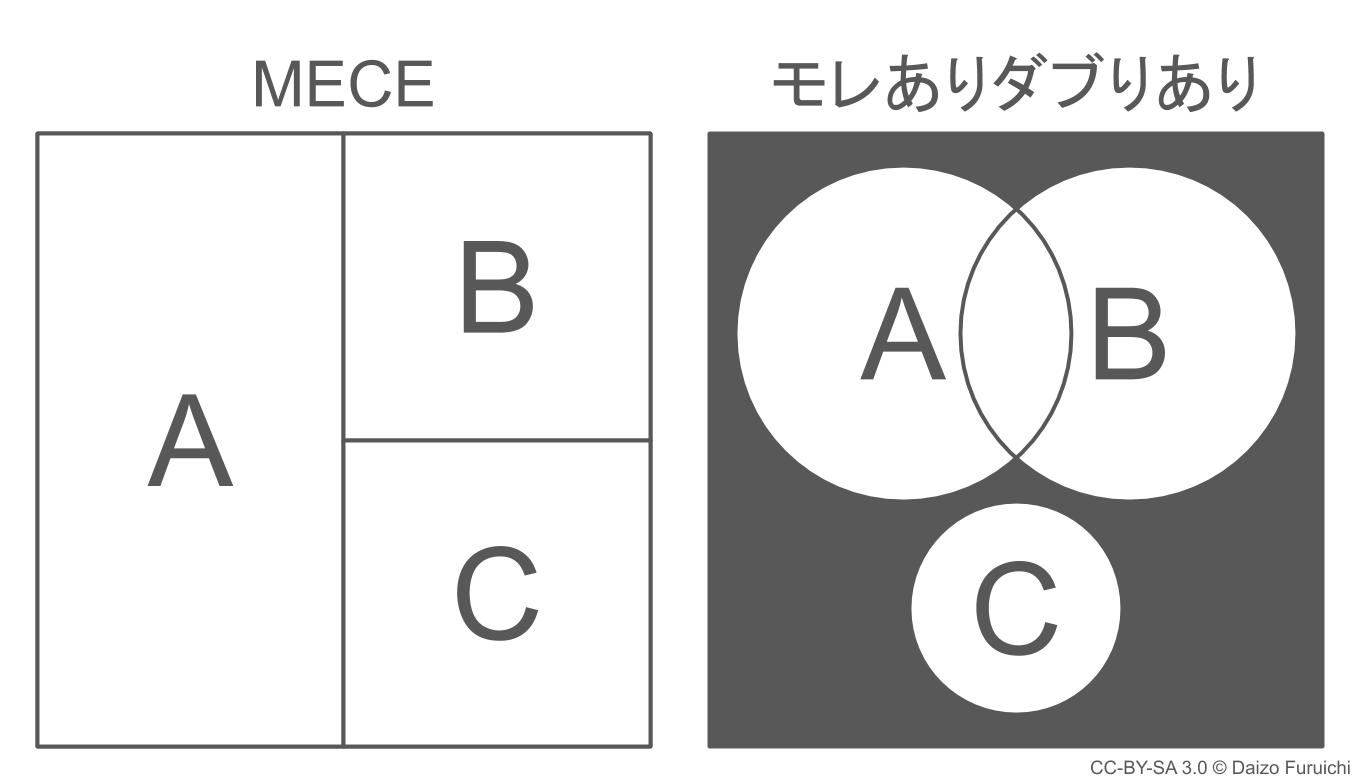
MECE（ミーシー）とは、「モレなくダブりなく」という意味のビジネス用語で、情報を論理的にわかりやすく整理するための手法です。MECEを使いこなすことで、ビジネスやプライベートで論理的思考（ロジカルシンキング）を実践できるようになります。
ここではMECEの切り口として、
- 因果関係：共通の結果をもたらす複数の原因を探す
- 類似性：共通の特徴を見つけてグループ化する
- 二項対立：互いに反する概念で２つに分ける
- 分割：全体を境界線で３つ以上に分割する
- 尺度：直線上に並んでいるものを任意の点で区切る
- プロセス：物事が起きる一連の流れを見つける
- 因数分解：出来事を掛け算の数式に変換する
の７つのパターンを、コンビニエンスストアを例題として具体的な例をご紹介します。
MECEの７つの切り口
MECE（モレなくダブりなく）は、コンサルタントのバーバラ・ミント氏が1973年に出版した著書「The Minto Pyramid Principle（ミントのピラミッド原則）」で世間に広まった考え方です。
ミント氏は身の回りの情報を、
- 因果関係によるグループ化
- 類似性によるグループ化
- 構造によるグループ化
の３つの方法でグループ化することができると説明しました。
そして３つ目の「構造によるグループ化」では、特に漏れがあったり重複したりすることが多いため気をつける必要があります。
そこで以前の記事では、ミント氏の考えをベースに筆者独自の「５つの構造化タイプ」をご紹介しました。
その５つの構造化タイプとは、
- 二項対立
- 分割
- 尺度
- プロセス
- 因数分解
です。
ここでは最初に紹介した「因果関係」「類似性」と合わせて、MECEの７つの切り口としてご紹介します。
また具体例として、架空のコンビニエンスストアを例題にそれぞれの切り口を考えてみたいと思います。
因果関係によるMECEの切り口
因果関係の切り口では、
- 共通の結果をもたらす複数の原因を探す
ことで、MECEを実現することができます。
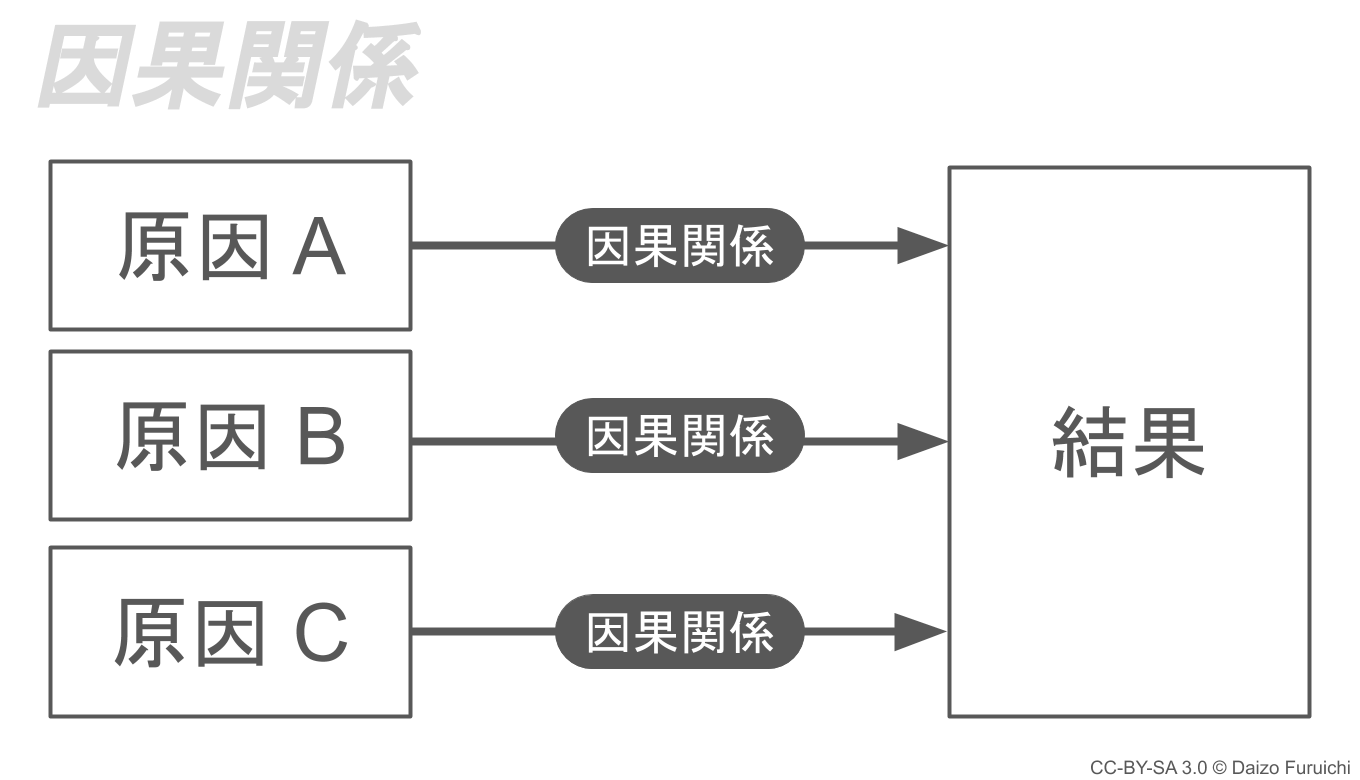
因果関係とは、「Xが原因となってYが起こる」といった関係のことを指します。
例えば「人材不足」という結果に対して、複数の原因となった重要な出来事を挙げることができれば、因果関係によるMECEと言えます。
コンビニを例として「店舗の人手不足」という結果を因果関係の切り口で分析すると、
- 原因A：近隣にある大学が定員割れするほど学生が減っている
- 原因B：向かいの敷地に競合他社のコンビニが出店した
- 原因C：求人に出しているバイトの時給が見劣りする
などが直接的な原因になります。
それぞれ「母数の減少」「人材確保の激化」「競争力の低下」といった異なる出来事ですが、「店舗の人手不足」という共通の結果をもたらしています。
この因果関係の切り口は、
- 全ての原因を挙げることができればモレがない
- 原因を個々のレベルに分解できればダブらない
ことになります。
もちろん、物事が起こる原因は大小様々で、すべてを網羅することが難しい時もあります。また複数の出来事が複雑に絡み合っていることもあります。
そういったときには、起きている出来事を小さく切り分けて、それぞれについて因果関係を考えてみてください。
類似性によるMECEの切り口
類似性の切り口では、
- 共通の特徴を見つけてグループ化する
ことで、MECEを実現することができます。
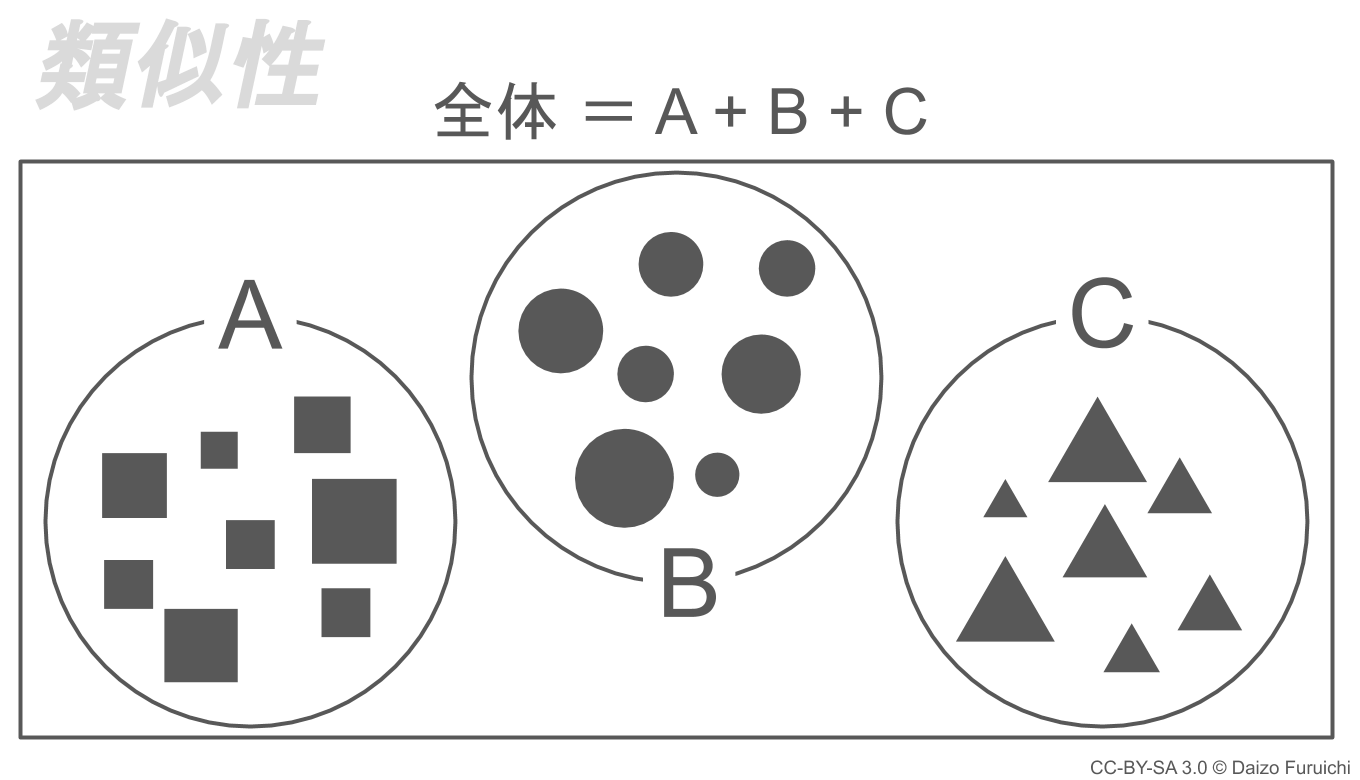
この切り口の考え方は非常にシンプルですが、全体をうまく説明することができる共通の特徴を見つけることが重要になります。
例えば「カゴに入った農作物」を、
- 野菜と果物に分ける
というような例が該当します。
この他にも、
- 色（カゴの中をオレンジ、黄、緑の色で分ける）
- 形（カゴの中を丸いもの、細長いもので分ける）
という類似性で分けることもできます。
この類似性の切り口では、
- そこにあるものが全てと定義すればモレがない
- それぞれの特徴を具体的に定義できればダブらない
ことになります。
今度はコンビニを例として「顧客の支払い方法」を類似性の切り口でMECEすると、
- 現金による支払い
- 磁気読み取りによる支払い
- IC読み取りによる支払い
- 二次元コード（バーコード・QRコード）読み取りによる支払い
となります。
コンビニが採用している支払い方法は決まっているので、現状で対応可能なものを挙げればモレはありません。しかし重複する特徴で分類してしまうと、ダブりが発生します。
例えば先ほどの例を、
- 現金による支払い
- カードによる支払い
- 二次元コード（バーコード・QRコード）による支払い
と分類してしまうと、MECEに失敗します。
なぜなら、
- カードに印刷されてるバーコードで支払う
という方法があるからです。
なぜこういったことが起きたかというと、最初のMECEは「読み取り方法」という同じ特徴で分類していました。（「現金による支払い」は「お金の目視による読み取りでの支払い」と置き換えます。）
一方で、次に挙げたMECEに失敗した例は、「形状」と「手法」という２つの特徴が混在してしまったために、ダブりが生じてしまったのです。
二項対立によるMECEの切り口
二項対立の切り口では、
- 互いに反する概念で２つに分ける
ことで、MECEを実現することができます。
この二項対立を使ったMECEの切り口では、項目が２つしか登場しないため比較的簡単に使うことができます。
例えば、
- A vs A以外
- A vs 反A
などが該当します。
この二項対立のMECEは、
- 「それ」と「それ以外」を足し合わせるとモレがない
- 全体から特定のものを抜き出しているのでダブらない
ことになります。
コンビニを例として「来店客」を二項対立の切り口でMECEすると、
- 過去に来店したことがある客 vs それ以外の客
- 目的があって来店した客 vs 何も目的がなく来店した客
などが考えられます。
このMECEの切り口をうまく使うコツとしては、
- かならず反対の定義を挙げる
ということです。
例えば、
- 目的があって来店した客 vs たまたま立ち寄った客
としてしまうと、一見問題がないように見えてもMECEに失敗しています。
なぜかというと、
- 目的があってたまたま立ち寄った客
というダブりが存在するからです。
このように完全に反対の事柄を設定しなければ、モレやダブりが生じてしまうかもしれません。
分割によるMECEの切り口
分割の切り口では、
- 全体を境界線で３つ以上に分割する
ことで、MECEを実現することができます。
この分割によるMECEの切り口は、先ほどの二項対立の発展系とも言えます。また類似性によるMECEとも似ていますが、こちらは初めから共通した特徴を持っていることが違います。
例えば、
- 地域の分割
- 空間の分割
- 部品の分割
などがイメージしやすいかもしれません。
この分割の切り口は、
- 全体を分割するだけなのでモレがない
- 境界によって分割されるのでダブりがない
ことになります。
コンビニを例として「出店エリア」を分割の切り口でMECEすると、
- 北海道
- 東北
- 関東
- 中部
- 近畿
- 中国
- 四国
- 九州沖縄
という八地方区分などが考えられます。他にも都道府県で分けてもMECEになります。
またコンビニの店内の売り場も、
- レジ横
- 雑誌・書籍棚
- ベーカリー棚…
などなど、空間をエリアごとに個別の名前をつけて分割することもできます。
さらに、一体となっているものを部品や部分で分けることも考えられます。
コンビニのレジにあるレジスターなら、
- 客側モニター
- 店員側モニター
- ハンディスキャナー
- ICカードリーダー
- 自動釣銭機
- レシートプリンター…
などなど、パーツに分けた切り口で、故障率や設備コストの分析ができるかもしれません。
このように全体を切り分けるタイプのMECEでは、モレることが少なく、分割できればダブることも起きにくくなります。
尺度によるMECEの切り口
尺度の切り口では、
- 直線上に並んでいるものを任意の点で区切る
ことで、MECEを実現することができます。
この尺度の切り口は、先ほどの「分割」という切り口の直線バージョンと考えると、イメージしやすいかもしれません。主に数字を使って尺度を表しているものに使いやすい方法です。
例えば、
- 年数
- 金額
- 距離
- 回数
- パーセンテージ
などで、このMECEがよく使われます。
この尺度の切り口は、
- 区切ったものを全て挙げればモレがない
- 基準になる点の前後で要素が分かれるためダブらない
ことになります。
コンビニを例として「最寄り駅からの距離」を尺度の切り口でMECEすると、
- 駅改札内、駅構内、500m未満、500m以上1km未満、1km以上3km未満、3km以上
のような分け方が考えられます。
また「来店客の年齢層」でMECEすれば、
- 10代、20代、30代、40代、50代、60代、70代以上
のようになるかもしれません。
ここで少し気になるのが、
- 区切りは等間隔である必要があるのか？
- 必ず全てを含めなければならないのか？
という点です。
まず「区切りは等間隔である必要があるのか？」という疑問に対しては、「必ずしも等間隔である必要がない」というのが答えです。
これは等間隔で区切ることに意味がある場合と、意味がない場合が存在しているためです。
等間隔で区切ることに意味があるのは、
- 区切りごとに中身を集計して比較する
ことが必要な場合などです。
先ほどの例の「来店客の年齢層」であれば、等間隔に区切ることで、それぞれの年齢層の来店客数を数値で比較することができます。
一方、等間隔で区切ることに意味がないのは、
- ビジネス上で意味のある区切りが存在している
場合などです。
例えば先ほどの例の「最寄り駅からの距離」については、仮に「500m以上1km未満」の店舗を同じグループとして扱う方が、ビジネス上の意思決定がしやすいと判断すれば、等間隔で区切る必要がありません。
いずれせよMECEを行う目的は、あくまで情報を整理して伝えやすくするためです。等間隔に区切ることで逆に伝わりにくくなるのであれば、それは避けなければなりません。
次に「必ず全てを含めなければならないのか？」という疑問ですが、こちらも「必ずしも含める必要はない」というのが答えです。
先ほどの「来店客の年齢層」では「10歳未満」の客層は存在していません。
これは一見「モレ」が生じているようにも見えますが、本当に「モレ」なのかどうかは、ビジネス上の意味で考えます。
もし仮にそのコンビニが、ファミリー層を攻略するために「10歳未満」の顧客の行動も重視する必要があれば、モレになります。
逆に、そのコンビニの主要顧客の年齢が高めで、「10歳未満」の顧客が滅多に来店しないのであれば、わざわざ区分けとして分類する必要がないかもしれません。
このように「なんのためにMECEをしようとしているか」を考えることで、抜け漏れに対する考え方も変わってきます。
尺度の切り口では「以下」と「未満」の使い分けに注意してください。
- 以上・以下：その数字を含む
- 未満：その数字を含まない
ということなので、
- 100個以下：0〜100個
- 100個未満：0〜99個
になります。
例えば、0〜299個まで分布しているものを尺度で切り分けると、
- 0個以上99個以下、100個以上199個以下、200個以上
- 0個以上100個未満、100個以上200個未満、200個以上
が同じ切り方になります。
プロセスによるMECEの切り口
プロセスの切り口では、
- 物事が起きる一連の流れを見つける
ことで、MECEを実現することができます。
このプロセスによるMECEの切り口は、先ほどの尺度のように直線的に並んでいるものを区切っていますが、その「区切り」が最初から存在している場合になります。また直線だけでなく、循環して戻ってくるような流れも含んでいます。
例えば、
- 直線的なプロセス（開始：A → B → C → D：完了）
- 循環的なプロセス（A → B → C → D → Aに戻る）
というような一連の流れです。
このプロセスの切り口は、
- 工程を全て挙げることができればモレがない
- 同時に２つの工程を通ることがなければダブらない
ことになります。
コンビニであれば、様々な作業手順がプロセスとして存在していますよね。
作業をプロセスごとにMECEで分ければ、各手順ごとに作業ミスが起こった場合の対処法をまとめることもできますし、過去のトラブルなどをわかりやすくまとめることができるかもしれません。
また、１つの作業と考えていたものを細い手順として分解すれば、それが「小さなプロセス」として認識できるようになります。そうすれば新しいスタッフを教育する場合に役立つかもしれません。
因数分解によるMECEの切り口
因数分解によるMECEは、
- 出来事を掛け算の数式に変換する
ことで、MECEを実現することができます。
因数分解とは、数学的には「足し算や引き算で表現された式を掛け算に直す」ことを指します。
ビジネスではその意味が転じて「ある物事を説明するために必要な要素を列挙する」場合に「因数分解する」という表現を使います。
この因数分解の切り口は、
- 全てを掛けたものが全体になるためモレがない
- 同じものを２回掛けない限りはダブらない
ことになります。
コンビニを例として「売上」を因数分解の切り口でMECEすると、
- 売上 ＝ 客数 × 客単価 × 来店頻度
というように表現できます。
「もっと売上をあげたい」という時に、単純に「売上」をそのままの状態で考えるのではなく、
- 客数
- 客単価
- 来店頻度
の３つに分解して考えることで、対策をより具体的に考えることができます。
さらに「客数」を掘り下げる場合には、
- 客数 ＝ 立地 × 天候 × 曜日
などとも表現できるかもしれません。
もちろんこのような式は、すべてを数値で表わせないので厳密には正しい数式ではありません。しかし、ビジネスで起こる出来事を、納得できる形で説明できていれば情報は伝わります。
MECEの切り口まとめ
ここまでの内容をまとめると、MECEの代表的なパターンとして、
- 因果関係：同じ結果をもたらす複数の原因を探す
- 類似性：共通の特徴を見つけてグループ化する
- 二項対立：互いに反する概念で２つに分ける
- 分割：全体を境界線で３つ以上に分割する
- 尺度：直線上に並んでいるものを任意の点で区切る
- プロセス：物事が起きる一連の流れを見つける
- 因数分解：出来事を掛け算の数式に変換する
の７つがあることがわかりました。
シンプルな事柄であれば、上記の７つのパターンのどれかにピッタリはまるものが見つかりやすいかもしれません。
しかし物事が複雑になってくると、１つのパターンに綺麗にはまるというのも少なくなります。そんな時には、より小さな出来事に分解して、それぞれに対して別々のMECEの切り口を考えてみましょう。
そして常に忘れてはいけないのは、
- 情報を整理して相手に伝わりやすくする
ためにMECEの切り口で考えている、という事です。
もしモレやダブりを無くすために、情報がちゃんと伝わらなくなってしまうなら本末転倒です。
むしろ言いたいことがちゃんと伝われば、多少のモレやダブりは問題になりません。このことを頭の隅に置きながら、MECEの７つの切り口を活用してみてください。
別の記事で、今回の７つの切り口が当てはまる経営フレームワークについてもまとめています。こちらも是非ご覧ください。
因果関係によるMECEとは？
因果関係を使ったMECEとは、
- 共通の結果をもたらす複数の原因
によって構成されたMECEのことです。
例えば、「店舗の人手不足」という結果に対して、「近隣人口の減少」「競合他社の出店」「バイト時給の競争力低下」といった異なる出来事が原因として挙げられる場合などが該当します。
類似性によるMECEとは？
類似性を使ったMECEとは、
- 共通の特徴によるグループ化
で構成されたMECEのことです。
例えば「カゴに入っている農作物」を、「果物と野菜に分ける」「色で分ける」「形状で分ける」といった共通する特徴でいくつかのグループに分ける場合などが該当します。
二項対立のMECEとは？
二項対立のMECEとは、
- 互いに反する２つの概念
で構成されたMECEのことです。
例えば「顧客」を「新規顧客（初めての客）」と「リピート客（初めてじゃない客）」に分けたり、「ブランドに好意的な顧客」と「ブランドに好意的ではない顧客」に分ける場合などが該当します。
分割によるMECEとは？
分割によるMECEとは、
- 全体を境界線で３つ以上に分割された要素
によって構成されたMECEのことです。
例えば、「日本」を都道府県で分割したり、「事務所」を「来客対応スペース」「執務エリア」「交流ラウンジ」などのエリアで分割したりする場合などが該当します。
尺度を使ったMECEとは？
尺度を使ったMECEとは、
- 任意の点で区切られた直線状の要素
によって構成されたMECEのことです。
例えば「金額」によって「5000円未満、5000円以上１万円未満、１万円以上」と区切る場合や、「来店回数」によって「１回だけ、２回、３回以上」と区切る場合などが該当します。
プロセスによるMECEとは？
プロセスによるMECEとは、
- プロセスを構成する一連の出来事
で形作られたMECEのことです。
例えば「作業手順」をステップごとに分割したり、何度も繰り返す「サイクル」をサイクルの状態ごとに分割する場合などが該当します。
因数分解によるMECEとは？
因数分解によるMECEとは、
- 出来事を掛け算で分解した場合の要素
で構成されたMECEのことです。
例えば「売上」を「客数 × 客単価 × 来店頻度」に分解する場合などが該当します。
おすすめの書籍
冒頭でお伝えした、ミント氏の著書はこちらになります。
この「新版 考える技術・書く技術」と併せて、入門書や練習問題をまとめた書籍も販売されています。
社会人として「情報を整理して伝える」という基本的な技術を身につけるために最適な本なので、ぜひ書店で見つけたら手にとってみてください。
