演繹法と帰納法の違いとは？図解と具体例でわかりやすく解説

演繹法と帰納法の違いを一言で表すと、

• すでに知っていることから想像するのが演繹法（えんえきほう）
• 起こった出来事からパターンを見つけるのが帰納法（きのうほう）

です。

わかりやすく図にすると、下記のようになります。

帰納法（きのうほう）は、起こった出来事から共通する部分を見つけ出し、パターンを理解することで、新たに起こった出来事の仮説（＝結論）を立てる方法です。

逆に演繹法（えんえきほう）は、すでに知られている「一般論」をベースに仮説（＝結論）を立てる方法です。どの一般論を使うかによって、立てる仮説（＝結論）の内容も大きく変わります。

しかし、仮説（＝結論）を立てる方法（推論）は、帰納法と演繹法だけではありません。

• 全然別の出来事だけど似ている部分を見つけて推測するアナロジー
• 演繹法とは逆に結果から出来事を推測するアブダクション

などが存在しています。

ここでは、演繹法と帰納法を含めた４タイプの推論を、わかりやすく解説します。

演繹法と帰納法の違い

演繹法（えんえきほう）そして帰納法（きのうほう）は、ロジカル・シンキング（論理的思考）でよく登場する言葉です。でも、どちらがどちらなのかわかりにくい用語ですよね。

それぞれ、

• 演繹法：一般論を使って出来事の結果を推測する
• 帰納法：複数の出来事とその結果から規則性を見つける

という違いがあります。

でも両方覚えようとすると面倒なので、

• パターンを見つける帰納法

だけ覚えておいてください。

それではもう一度図を見ながら、違いを確認していきましょう。

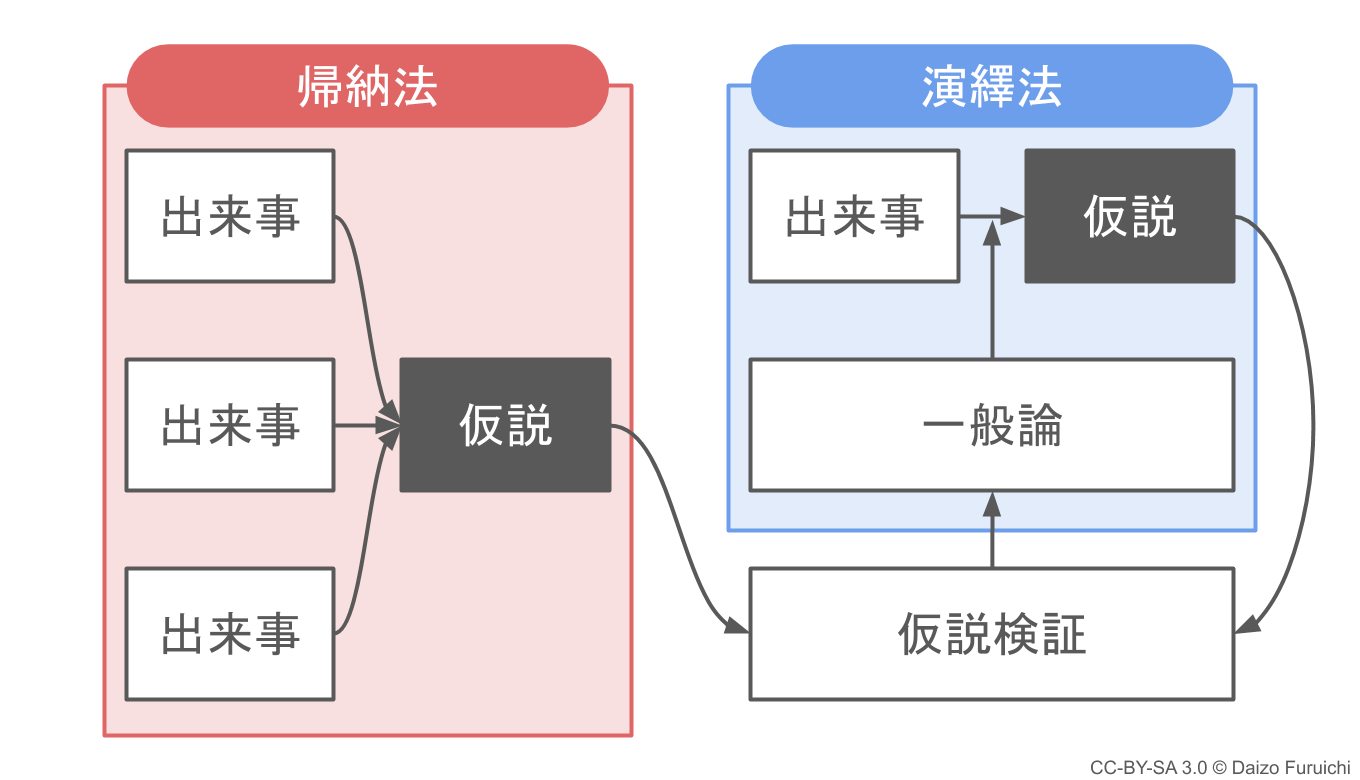
まず帰納法（きのうほう）を見てみると、起こった出来事だけで仮説を立てることができるのがわかります。

例えば、

• 出来事：一昨日はミカンが５つ売れた
• 出来事：昨日はミカンが５つ売れた
• 出来事：今日もミカンが５つ売れた
• 仮説：だからこの時期は毎日ミカンが５つ売れるだろう

というのが帰納法の考え方です。

すでにわかっていることが判断のベースになるので、パターンさえ見つかれば推測することができます。逆にまだ起こっていないことは、帰納法で推測することができません。

一方で演繹法（えんえきほう）は「一般論」を必要とします。すでにわかっていることから理論を展開するので、仮説の精度は帰納法より高くなります。

例えば過去数年のデータから、

• この時期には毎日ミカンが5つ売れる

ということがわかっていれば、それを推測の根拠に使います。

そのため論理の展開は、

• 一般論：この時期には毎日ミカンが5つ売れる
• 出来事：今日もミカンが売れている
• 仮説：だから今日は５つのミカンが売れるだろう

となります。

ここで注意しなければならないのは、推論はあくまで「仮説」だということです。「仮説」は「仮説検証」することで「一般論」になります。

このように、演繹法と帰納法の大きな違いは、すでにわかっていることである「一般論」を推測に使うかどうかになります。

４タイプの推論

ここまでご紹介した演繹法と帰納法の他にも、物事を推測するための手法が存在しています。

演繹法と帰納法を含めた代表的なものが、

• 演繹法：一般論を使って出来事の結果を推測する
• 帰納法：複数の出来事とその結果から規則性を見つける
• アナロジー：別の似ている事例から結果を推測する
• アブダクション：結果と一般論から起こった出来事を推測する

の４つです。

演繹法

ここからはもう少し踏み込んで、複数の具体例を踏まえて解説していきたいと思います。繰り返しの説明になっている箇所もあるので、軽く読み飛ばしつつ読み進めてください。

演繹法とは、

• 一般論を使って出来事の結果を推測する

思考法です。

英語では「Deductive Reasoning（ディダクティブ・リーズニング）」「Deductive Logic（ディダクティブ・ロジック）」「Logical Deduction（ロジカル・ディダクション）」などと呼ばれます。

図で表すと、下記のようになります。

演繹法では、

• AならばB

ということがわかっている時に、「A」が起これば「B」になることが予測できます。

まず簡単な例を挙げてみましょう。

あなたは「プロ野球チームの球団Aが負けた日の翌日は上司の機嫌が悪い」という「一般論」を知っていたとします。

これは上司自身も飲みの席で公言している内容であり、部署内の誰もが知っている一般常識に近い理論です。

そしてある日の晩、球団Aが試合に負けました。

あなたは、

• 一般論：球団Aが負けた日の翌日は上司の機嫌が悪い
• 出来事：球団Aが試合に負けた
• 仮説：明日は上司の機嫌が悪いかもしれない

と考えます。これが演繹法（えんえきほう）を使った典型的な考え方です。

もう一つビジネスでの具体例を挙げます。

もし、

• 一般論：自社店舗の近くに競合が出店すると売上が減る
• 出来事：自社店舗の近くに競合が出店した

となった場合、あなたはどのような仮説を立てるでしょうか？

この場合は、

• 仮説：自社店舗の売上が減るかもしれない

という仮説になると思います。

こういった仮説や予測は、日々のビジネスの場面でよく見かけると思います。

社内プレゼンテーションの場で「エビデンスは？（根拠は？）」などと聞かれそうな時には、過去の統計データなどを使って演繹法で説明すれば説得力が上がります。

三段論法

演繹法を発展させた手法に「三段論法」というものがあります。

三段論法は、

• 大前提
• 小前提
• 結論

で構成されています。

これは演繹法だと、

• 一般論 ＝ 大前提
• 出来事 ＝ 小前提
• 仮説 ＝ 結論

にそれぞれが相当します。

例えばあなたが、社内報告で「円安の影響で原料のコストが上がっている」ことを伝えたいとします。

これを三段論法に当てはめると、

• 大前提：円安になると原料を輸入するコストが上がる
• 小前提：現在の為替は円安方向に振れている
• 結論：原料の調達コストが上がるだろう

となります。

このように、

1. 「大前提」でお互いの前提条件や事前の知識をそろえる
2. 「小前提」で出来事をシンプルに説明する
3. 「結論」で相手に伝えたいことを簡潔に述べる

という手順を踏めば、ビジネスシーンで物事をすっきりとわかりやすく伝えることができます。

帰納法

帰納法とは、

• 複数の出来事とその結果から規則性を見つける

思考法です。

英語では「Inductive Reasoning（インダクティブ・リーズニング）」などと呼ばれます。

図で表すと、下記のようになります。

帰納法では、

• A ならば B

ということが何度か起こると、「A ならば B」というパターンを発見することができます。

この帰納法は、狭義では「枚挙的帰納法」とも呼ばれたりします。根拠になる事例を「枚挙する（いくつも挙げる）」ことで推論を行うためです。

例えば、もしあなたが「株式投資」に興味がった時、

• 出来事：同僚の買った株が上昇して「儲かった」と言っている
• 出来事：友人の買った株が上昇して「儲かった」と言っている
• 出来事：ニュースで株を買って儲かった人がたくさんいると言っている

ということが起こった場合に、どのような推論をするでしょうか？

帰納法であれば、

• 仮説：株を買ったら株価が上昇して儲かる

という推測をしてしまうかもしれません。

ただし、これはあくまで「仮説」であり、「株を買うと儲かる」という因果関係を証明するものではありません。周りにつられて高値の株式に手を出してしまうと、大損をしてしまうかもしれません。（もちろんその仮説が当たって、一緒に儲かる可能性もあります。）

ここで先ほど説明した「演繹法」を思い出してみましょう。

もし、

• ニュースで株で儲かった人の話題が出る頃が株価のピーク

という「一般論」を、あなたが知っていたとします。

そうなると、

• 一般論：ニュースで株で儲かった人の話題が出る頃が株価のピーク
• 出来事：ニュースで株で儲かった人の話題が出た
• 仮説：今が株価のピーク（いま買っても儲からない）かもしれない

という推測をするかもしれません。

このように、帰納法で考えるか演繹法で考えるかで結論は大きく変わるのです。

ここからはビジネスの場面を想定して、別の具体例を挙げてみます。

先ほどの演繹法の具体例では、

• 自社店舗の近くに競合が出店すると売上が減る

という一般論を例に考えてみました。

しかし、このようなビジネスでのノウハウや情報などは、最初からすべてわかっているわけではありません。初めて挑戦することや前例のないことから将来を予測する場合は、「帰納法」を使うことがほとんどになると思います。

もし「競合の出店の影響」がまだ分かっていない時点では、

• 出来事：自社店舗1号店の近くに競合が出店して売上が減った
• 出来事：自社店舗2号店の近くに競合が出店して売上が減った
• 出来事：自社店舗3号店の近くに競合が出店して売上が減った

という同じような事例がいくつか観察できた後に、

• 仮説：自社店舗の近くに競合が出店すると売上が減る

という仮説を立てることができるようになります。

そしてこの「仮説」がその後の事例も含めて、統計データなどで裏付けができた時に「一般論」として使えるものになります。

このような「仮説」→「一般論」という流れは、ビジネスの場でよく見かけることができます。

例えば、ある食品スーパーの「購買データ」から、

• 白菜を買う人は鍋用スープも買うことが多い

ということが分かったとします。

ここから、

• 野菜売り場の白菜コーナーの横に鍋用スープをおけば売れる

という仮説を立てることができます。

そして実際に店頭で実験してみる（仮説検証する）ことで、その仮説が正しいかどうか判断できます。

もしその仮説が正しければ、新しいノウハウとして別の店舗での「一般論」として、店舗レイアウトの提案に使うことができるようになります。

帰納法と営業資料

取引先に新しい商品を進める時に役立つのが、「導入事例」や「お客様の声」などの営業資料ですよね。

実際に営業として活動されている方は、効果があるかどうかわからないものを売ることが、いかに大変かを実感されているんじゃないでしょうか。

新しい商品をすすめると取引先は、

• 「で、うちの売り上げは上がるの？他社の事例はないの？」
• 「コスト削減に本当に効果があるの？すでに導入してる会社はどうなの？」

などと聞いてきます。

その時に「導入事例」や「お客様の声」をまとめた資料があれば、受注の可能性は一気に上がります。

その理由は、取引先の担当者が、営業資料の内容を材料に勝手に推論を行なってくれるからです。

一番望ましいのは、裏付けがある「演繹法」での説明です。

過去の統計データから「導入企業の〇〇%がコスト削減に成功しました！」なんて言えたら説得力があります。しかし、演繹法で使えるような根拠（一般論）が手に入るまでには時間がかかるので、初期の営業活動では使えません。

そこで登場するのが「帰納法」を使った説明です。

帰納法では、いくつかの少ない事例があれば、受け手の方が「うちの会社も成功事例のようになるかも」という仮説を立ててくれます。

その成功事例が、たとえ導入した10社のうちたまたま上手くいった3社の事例だったとしても、受け手がそのことを知らなければ「成功する」という推論に誘導することができます。

もちろん、情報操作をすることはあまりよくないことです。しかし逆の立場になることを考えれば、悪意のある会社の「帰納的営業資料」や「帰納的広告」にダマされることを防げるかもしれません。

このことを頭に入れた上で「導入事例」や「お客様の声」を上手く使って、商品の価値を伝えるようにしてみてください。

アナロジー

アナロジーとは、

• 別の似ている事例から結果を推測する

思考法です。

「類推」とも呼ばれる推論方法で、英語では「Analogy」と書きます。

図で表すと、下記のようになります。

アナロジーでは、

• A ならば B

ということが分かっている状態で、「A」に似ている「C」が現れた時に、

• C ならば B

も成り立つという仮説を立てる方法です。

例えばあなたが、

• 競合X店の近くに別の競合Y店が出店したらX店の客足が減った

という情報を知っていたとします。

そして、

• 自社店舗と競合X店は似ている

という事実があった場合には、

• 既知の事例：競合X店の近くに別の競合Y店が出店したらX店の客足が減った
• 出来事：自社店舗と競合X店は似ている
• 仮説：自社店舗の近くに競合Y店が出店したら自社店舗の客足が減るだろう

という仮説を導くことができます。これが「アナロジー」での考え方になります。

アナロジーは、イノベーションや業界の常識をひっくり返すような戦略にも使われます。

例えば、パナソニックの創業者である松下幸之助氏は「水道哲学」と呼ばれる考え方を持っていました。

水道哲学とは、

• 既知の事例：水道水は大量に安く供給されるので誰の手にも行き渡って人々を幸せにする
• 仮説：産業製品も大量に安く供給することで誰の手にも行き渡って人々を幸せにする

というアナロジーになります。

この水道哲学の考え方をベースに、1950年代には「家電製品の大量生産」と日本初の「系列電気店ネットワーク 」を組み合わせることで、手頃な価格の家電製品を日本中どこでも蛇口をひねるように手に入れることができるようになりました。

このように、他の業界の「常識」を自分たちの業界の「非常識」に当てはめることで、新しい戦略を生み出すことができます。

アブダクション

アブダクションとは、

• 結果と一般論から起こった出来事を推測する

思考法です。

「仮説推論」とも呼ばれる推論方法で、英語では「Abductive Reasoning（アブダクティブ・リーズニング）」などとも呼ばれます。

図で表すと、下記のようになります。

アブダクションは一見すると演繹法とそっくりですが、

• 演繹法：結果を推測する
• アブダクション：起こった出来事を推測する

という点が違います。

• A ならば B

ということがわかっている時に、「B」という結果が得られた場合には「A」が起こったことを推測することができます。

これは、

• 推理小説に出てくる探偵

をイメージするとわかりやすいかもしれません。

探偵は殺人現場に残された証拠や様子を観察し、過去の経験や知識と照らし合わせることで、その場所で起こったことを推測します。

ビジネスでの具体例を挙げると、

• 一般論：自社店舗の近くに競合が出店すると売上が減る
• 結果：自社店舗の売上が減った
• 仮説：自社店舗の近くに競合が出店したのかもしれない

という推測です。

最初にご紹介した演繹法の、

• 一般論：自社店舗の近くに競合が出店すると売上が減る
• 出来事：自社店舗の近くに競合が出店した
• 仮説：自社店舗の売上が減るかもしれない

という推測と比べてみると、違いがわかりやすいと思います。

この「アブダクション」という考え方は、ビジネスの場では原因究明や課題発見によく使われます。

• 機械設備の故障原因の究明
• ヒヤリハットの事例報告
• 受注・失注案件の分析
• 離職率上昇の原因分析

などなど、すでに起こった出来事に対する分析に役立ちます。

４つの推論の注意点

今回は、

• 演繹法：一般論を使って出来事の結果を推測する
• 帰納法：複数の出来事とその結果から規則性を見つける
• アナロジー：別の似ている事例から結果を推測する
• アブダクション：結果と一般論から起こった出来事を推測する

という４タイプの推論をご紹介しました。

これらの推論は、上手く使えば精度の高い推測をすることができます。その一方で、洞察力に欠けていたり、一般論の選び方を間違うと、役に立たない精度の低い推測になってしまうこともあります。

一般論を使う「演繹法」「アナロジー」「アブダクション」の注意点としては、

• 最初に思いついた一般論に固執しすぎない
• 常識と思っていた一般論も覆されることがある
• 一般論が変われば仮説も大きく変わってしまう

などです。

特に「一般論」が「業界の常識」のような凝り固まったものである場合は、他社の常識破りの戦略に足元をすくわれてしまうかもしれません。そのため、根拠となる一般論を考える時には、より広い視野を持った上で根拠を選ぶ必要があります。

また「帰納法」の注意点としては、

• 新しい事例で仮説が簡単に書き換わってしまう

ことです。

帰納法の考え方では、これまでに起こったことや、自分で観察している範囲でしか仮説を立てることができません。そのため、新しい情報や新しい視点には非常に弱い推論です。

このような帰納的な考え方の弱点を補うためには、別の事例に共通点を探す「アナロジー」などが役に立つかもしれません。自分の業界で前例がなくても、別の業界で前例が作られている可能性があります。

ここまでご紹介した４タイプの推論は、それぞれに上記で挙げたような注意点が存在しています。ビジネスシーンではそれぞれの特徴を理解した上で、複数を組み合わせて使うことで、より精度の高い推論ができるようになります。

関連書籍

論理的文章作法〈帰納法・演繹法・弁証法で書く〉 (〈型〉で書く文章論)

西田みどり

1,980円(04/08 22:48時点)

発売日: 2017/10/23

Amazon楽天市場

Amazonの情報を掲載しています

そもそも「論理的に考える」って何から始めればいいの？

深沢真太郎

1,386円(04/08 22:48時点)

発売日: 2015/12/10

Amazon楽天市場

Amazonの情報を掲載しています

入門 考える技術・書く技術――日本人のロジカルシンキング実践法

山崎 康司

1,650円(04/08 17:22時点)

発売日: 2011/04/08

Amazon楽天ブックス

Amazonの情報を掲載しています