だいぞう
だいぞう
「経験効果」「エクスペリエンス・カーブ」とも呼ばれ、製造業だけでなくサービス業でも同様の効果が現れます。
簡単に言えば、
- 何回も同じものを作れば慣れてスピードが上がる
- 何回も同じものを作れば失敗しなくなる
という効果です。
そしてその効果の度合いを「習熟率」と呼びます。
経験曲線効果とは?
経験曲線効果(Experience Curve Effects、エクスペリエンス・カーブ・エフェクト)では作業の経験が2倍になるにつれて、ほとんどの業種で製品1つあたりの平均費用が10〜25%ほど下がると言われています。
この効果は1966年に、アメリカのコンサルティング会社「BCG(ボストン・コンサルティング・グループ)」のブルース・ヘンダーソン氏が、企業研究によって発見したそうです。
この下がる割合を「習熟率」と呼びます。下の図は習熟率80%の場合(20%減少)で、累積の生産量が Q1 から Q2 に倍増した時のグラフです。
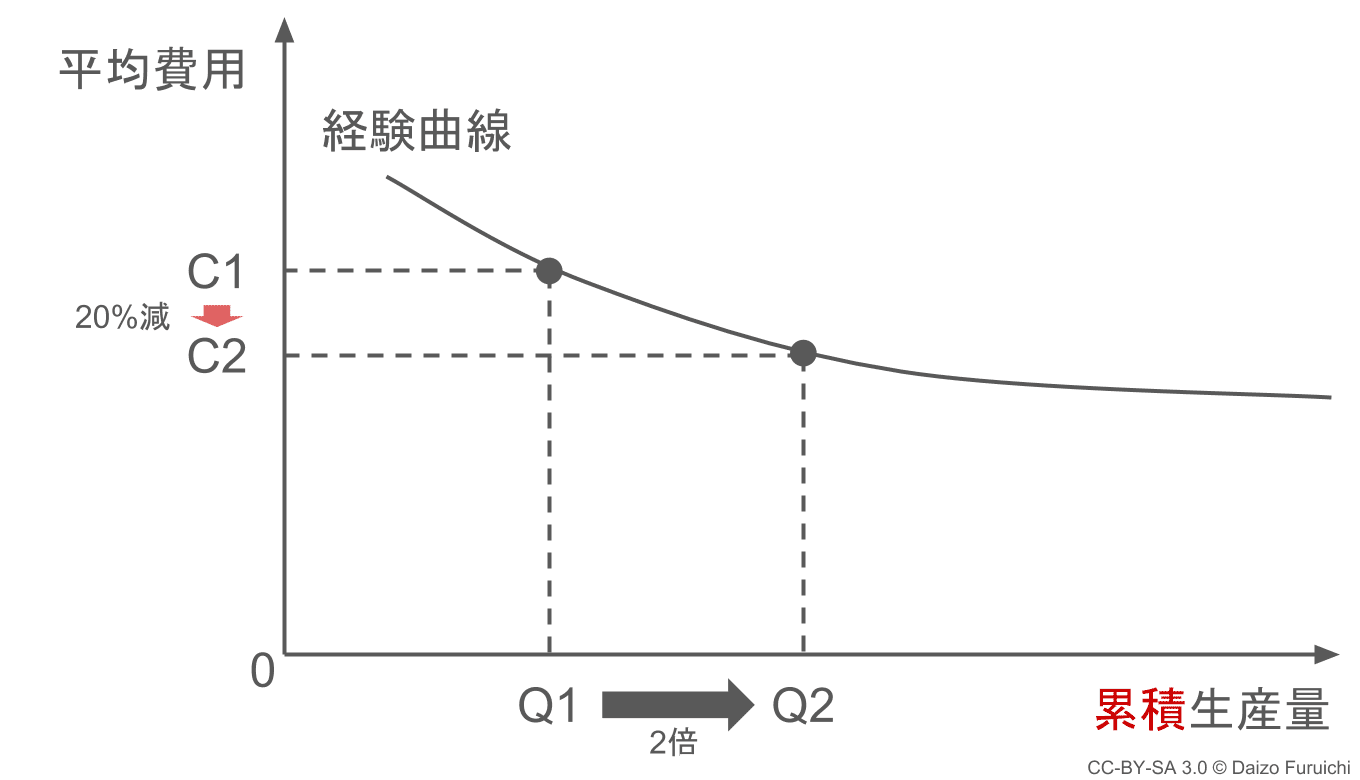
ここで注意が必要なのは「累積」の生産量ということです。
同じ製品を作り続ければ「累積」になり、工場を増やしても経験曲線効果は引き継ぐことができます。しかし別の製品を作り始めると「累積」にならないため、経験曲線効果は引き継ぐことができません。
サービス業でも同じで、チェーン展開をすれば経験曲線効果が発揮されます。しかし全く違う業態で店舗を増やすと、経験曲線効果はほとんど現れません。
経験曲線と学習曲線の違い
ちなみに「学習曲線」という言葉もありますが、経験曲線は学習曲線の考え方をベースに発展させたものです。そのため「学習曲線 = 経験曲線」として語られる場合もあります。
学習曲線は「練習量」と「反応速度」による曲線で、「何度も解いた問題はすぐに取りかかれる」ような状態になることを指します。
例えば組み立て部品を与えられた時に、
- えーっと…、どこから取り付けるんだっけ?
という考える時間がどんどん減るのが「学習曲線」です。
経験曲線効果で平均費用が下がる理由
誰でも初の作業は、時間がかかるものです。しかし5回目の同じ作業と10回目の同じ作業では、10回目の作業の方が5回目の時より早く終わったりします。
さらに同じ作業を続ければ、作業を始めた時に比べて随分と早く作業ができるようになるかもしれません。また似たような作業であれば、以前の経験を生かすことが出来るので初めてでも早く作業ができます。
このような効果で、人件費が減ったり不良品の処分費用が減って、結果的に平均費用が下がっていきます。
経験曲線効果で平均費用が減る理由は、労働者の効率向上以外にも次のようなものがあります。
- 作業手順や方法が改善されて効率が上がる
- 装置や器具が改良されて生産性が上がる
- 製品設計の見直しで生産効率の向上や不良率の低下が実現する
- トラブルの解決が早くできるようになる
- トラブルそのものが減ってくる
例えば、工場である製品を生産していたとします。その工場では製品を作れば作るほど経験が蓄積され、効率的に生産できるようになります。
その後、同じ製品を作る同じ設備の工場を、もう一つ別の場所に作ったとします。そうすると作る製品もそのための設備も同じであるため、最初の工場の改善ノウハウをそのまま活かすことができます。
2つ目の工場は改善後の効率が良い状態からスタートするので、最初から経験曲線効果が効いた状態で生産を始めることができます。
これをグラフで表してみましょう。
下の図は、平均費用と生産量のグラフです。最初の工場で生産量 Q を生産した時の平均費用を C1 とします。
生産をすることで経験やノウハウが累積されて、平均費用のグラフは全体的に下がってきます(薄い曲線から濃い曲線に移動します)。
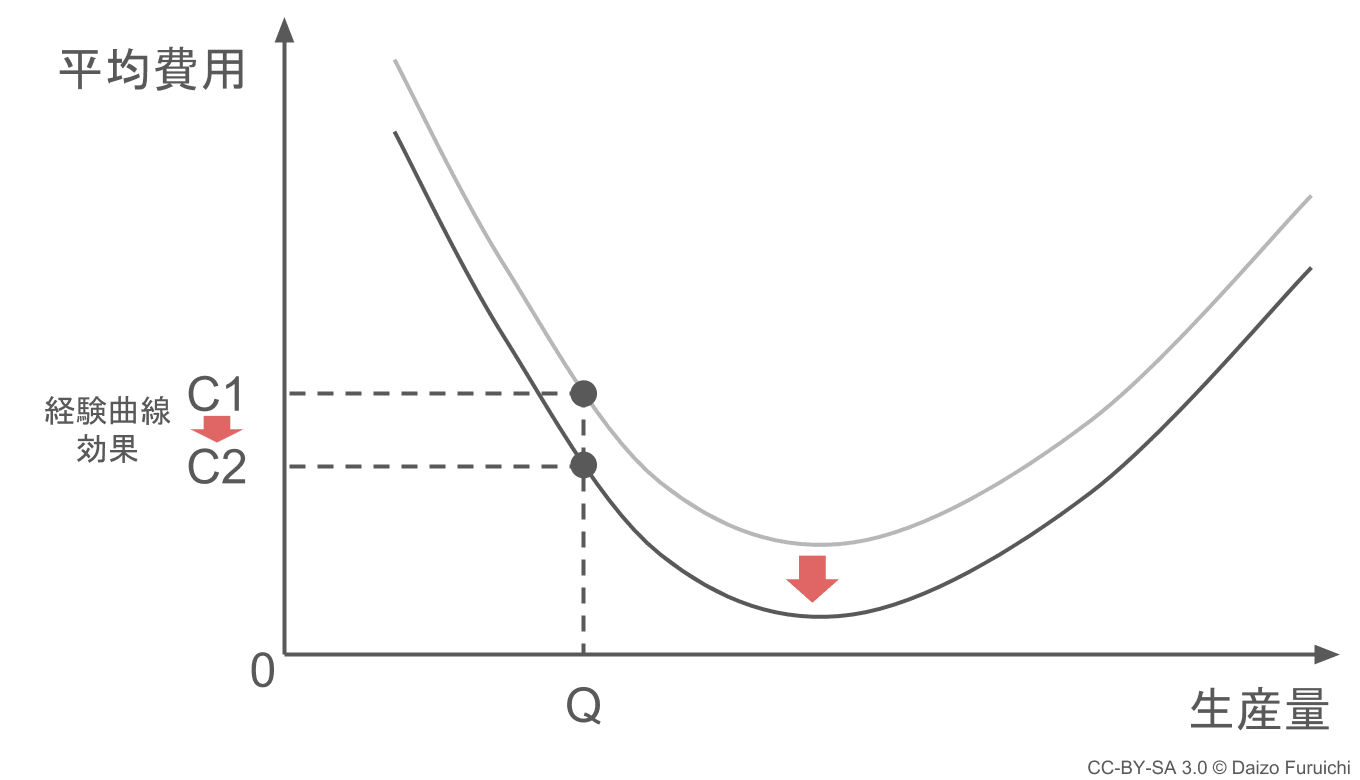
そして同じ製品を同じように作る2つ目の工場を稼働させた時には、最初の工場の経験曲線効果で平均費用が下がった状態でスタートできます。これが経験曲線効果のメリットです。
つまりすでにグラフが下にさがっているので(濃い曲線のある位置)、2つ目の工場で生産量 Q を生産すると最初から平均費用 C2 で生産することができます。これが経験曲線の効果です。