構造化による5つのタイプの具体例
ここからは特にMECEを意識する必要がある、「構造によるグループ化」の5つのタイプをご紹介します。
MECEの5つの構造化タイプとは、
- 二項対立
- 分割
- 尺度
- プロセス
- 因数分解
です。
ちなみにこの5つの分類は筆者独自のまとめ方で、ミント氏の理論をベースに、自身のコンサルティング経験などを踏まえて分類してみました。
二項対立
まず一番わかりやすくて一番簡単なMECEは「二項対立(にこうたいりつ)」です。
二項対立とは、「A」と「A以外のもの」という一方とその反対もので表現できる分け方です。
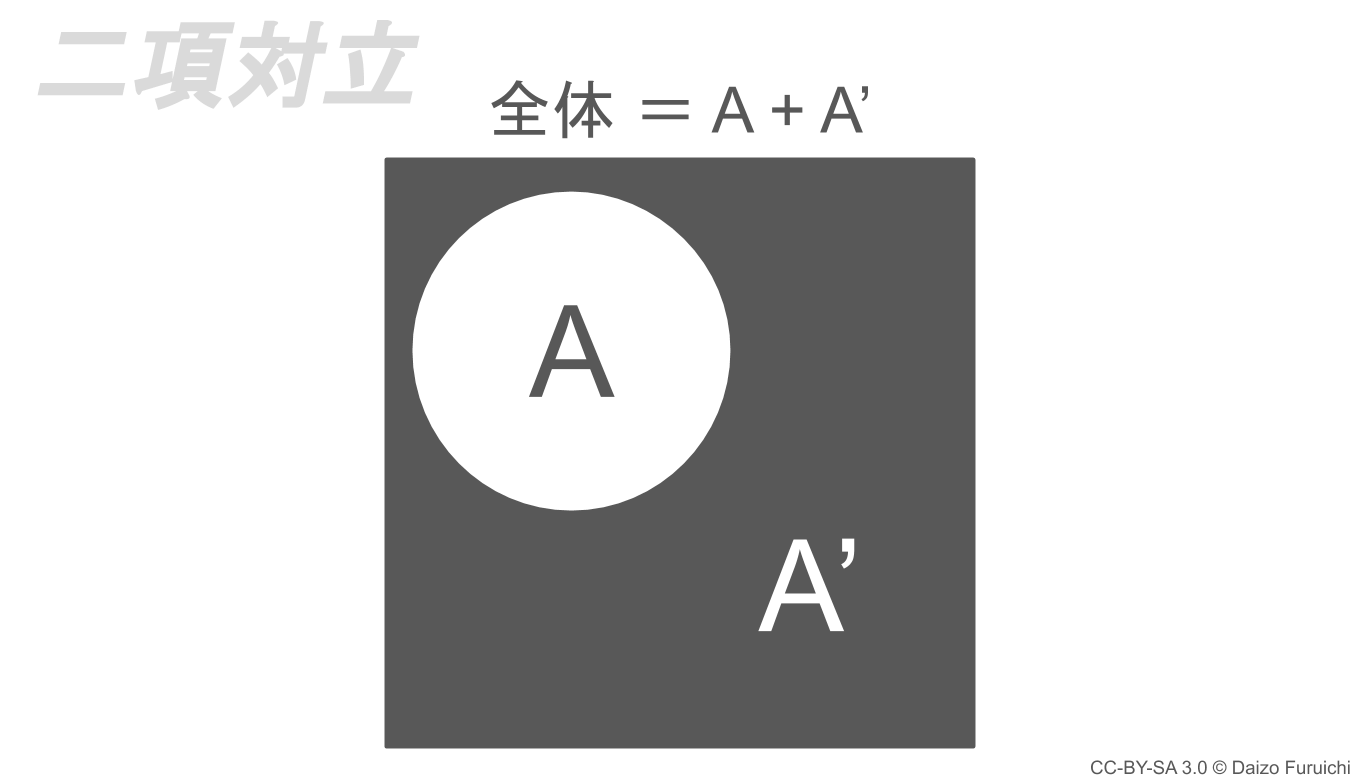
この「二項対立」では、
- 「それ」と「それ以外」を足し合わせるとモレがない
- 全体から特定のものを抜き出しているのでダブらない
ことでMECEが実現できます。
具体例としては、
- 売上全体の半分以上を稼ぎ出す製品 vs それ以外の製品
- 自社商品を使用したことがある消費者 vs それ以外の消費者
- 直営店がある市町村 vs 直営店のない市町村
など色々と考えられます。
分割
次は全体を3つ以上に分けるMECEで、「分割」と呼ばれるタイプです。
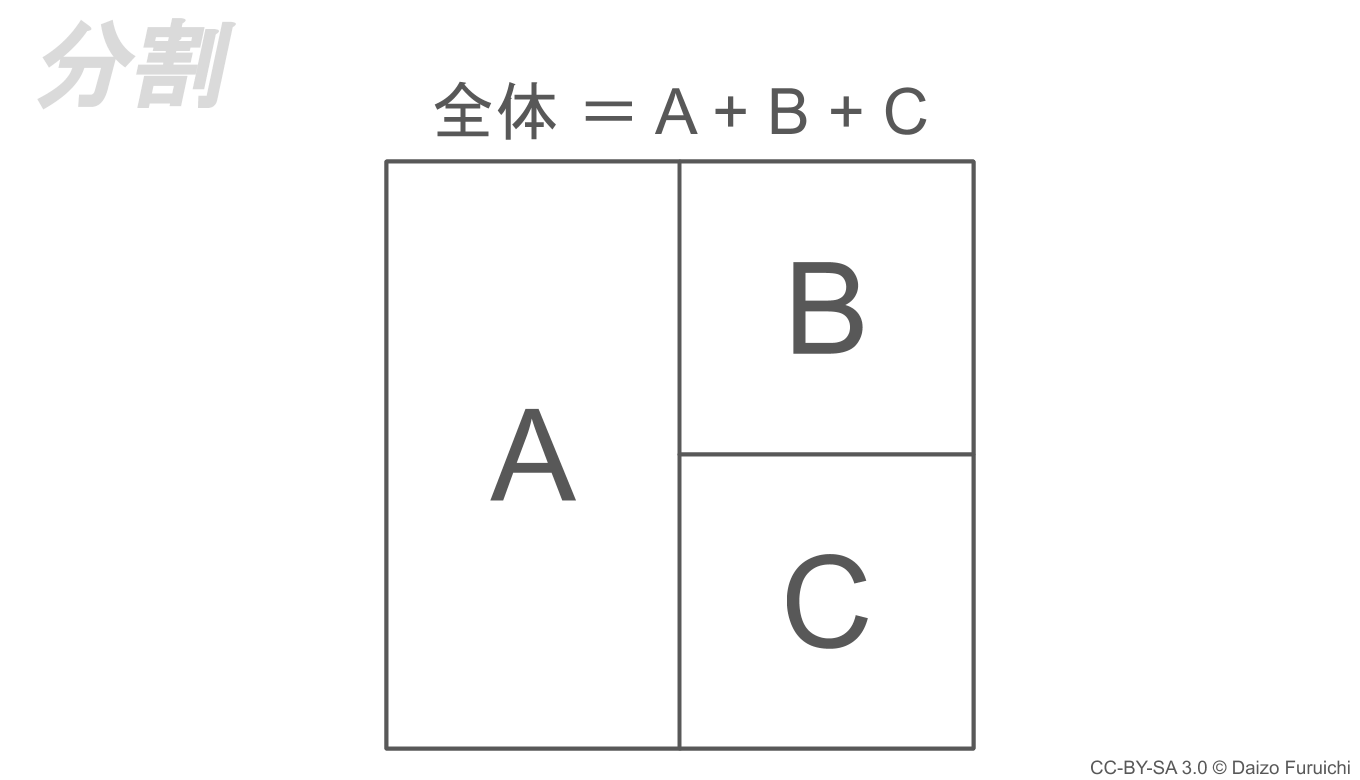
この「分割」では、
- 全体を分割するだけなのでモレがない
- 境界によって分割されるのでダブりがない
ため、MECEが実現できます。
具体例としては、
- 組織図
- SBU(戦略的事業単位)
- 製品X = 部品A + 部品B + 部品C
- 経営資源 = ヒト + モノ + カネ + 情報
- 売上 ー 原価 = 粗利
などが考えられます。
尺度
「尺度」と呼ばれるタイプは、要素が一本の線状に並んでいることが特徴です。
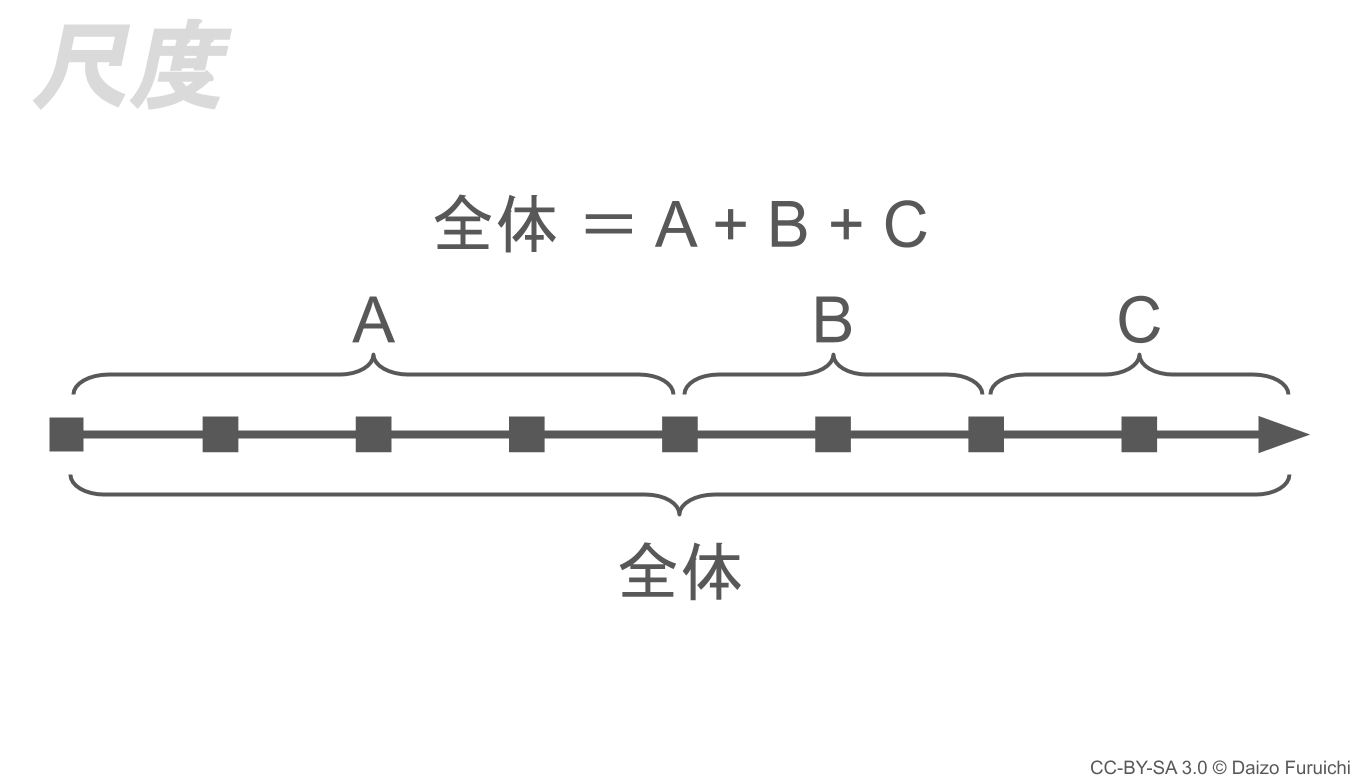
この「尺度」では、
- 区切ったものを全て挙げればモレがない
- 基準になる点の前後で要素が分かれるためダブらない
ため、MECEが実現できます。
具体例としては、
- 年齢:10代、20代、30代…など
- 温度:〜5℃、5〜15℃…など
- 年収:〜300万円、301〜500万円…など
などが考えられます。
プロセス
一連の流れや、循環するような流れで表現できるものを「プロセス」と呼びます。
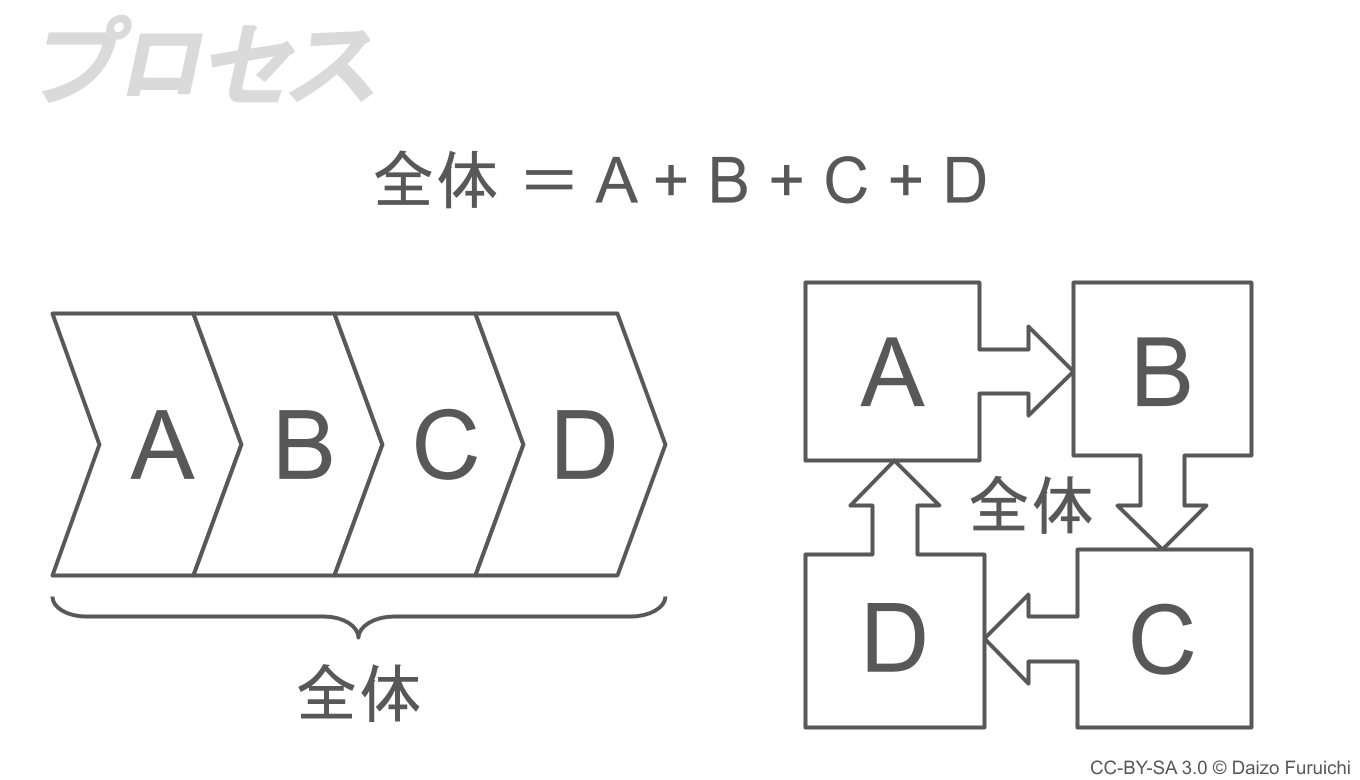
この「プロセス」では、
- 工程を全て挙げることができればモレがない
- 同時に2つの工程を通ることがなければダブらない
ため、MECEが実現できます。
具体例としては、
- 組み立て工程
- PDCAサイクル
- 旅行の日程
などが考えられます。
因数分解
ここまで紹介した4つは「足し算」の式で表すことができますが、最後にご紹介するタイプは「因数分解」です。これは物事を「掛け算」で表すMECEです。
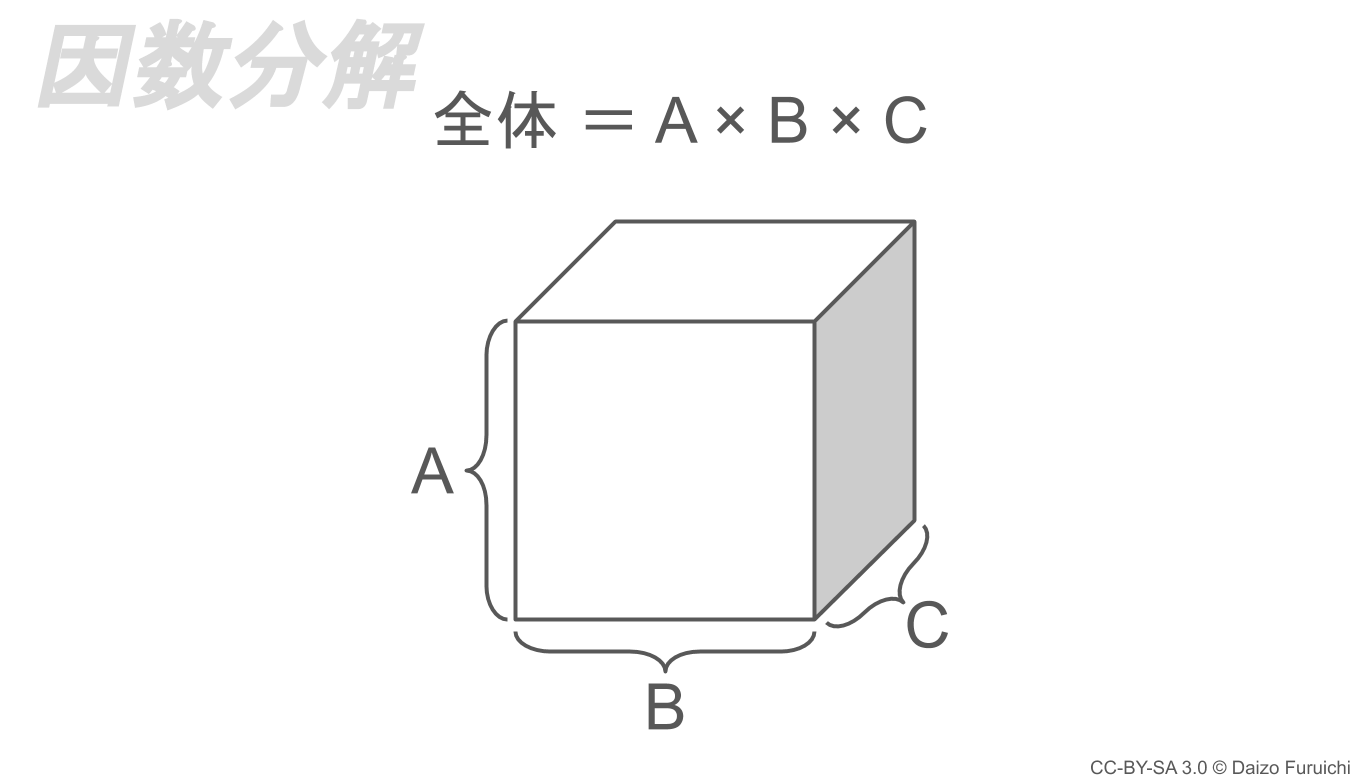
この「因数分解」では、
- 全てを掛けたものが全体になるためモレがない
- 同じものを2回掛けない限りはダブらない
ので、MECEが実現できます。
具体例としては、
- 売上 = 客数 × 客単価 × 来店頻度
- 成約率 = 問い合わせ率 × 商談率 × 受注率
などが考えられます。