タイミー初期成長の秘密:密度の経済とクリティカルマスの制御
タイミーは、2018年8月2日に正式サービスがリリースされました。
しかし対象となる地域は、東京都の渋谷エリアのみ。非常に限られた範囲からのスタートです。
前述したように、タイミーのビジネスモデルでは、店舗と求職者の双方が価値を高め合う「間接的ネットワーク効果(外部性)」を生み出す必要があります。
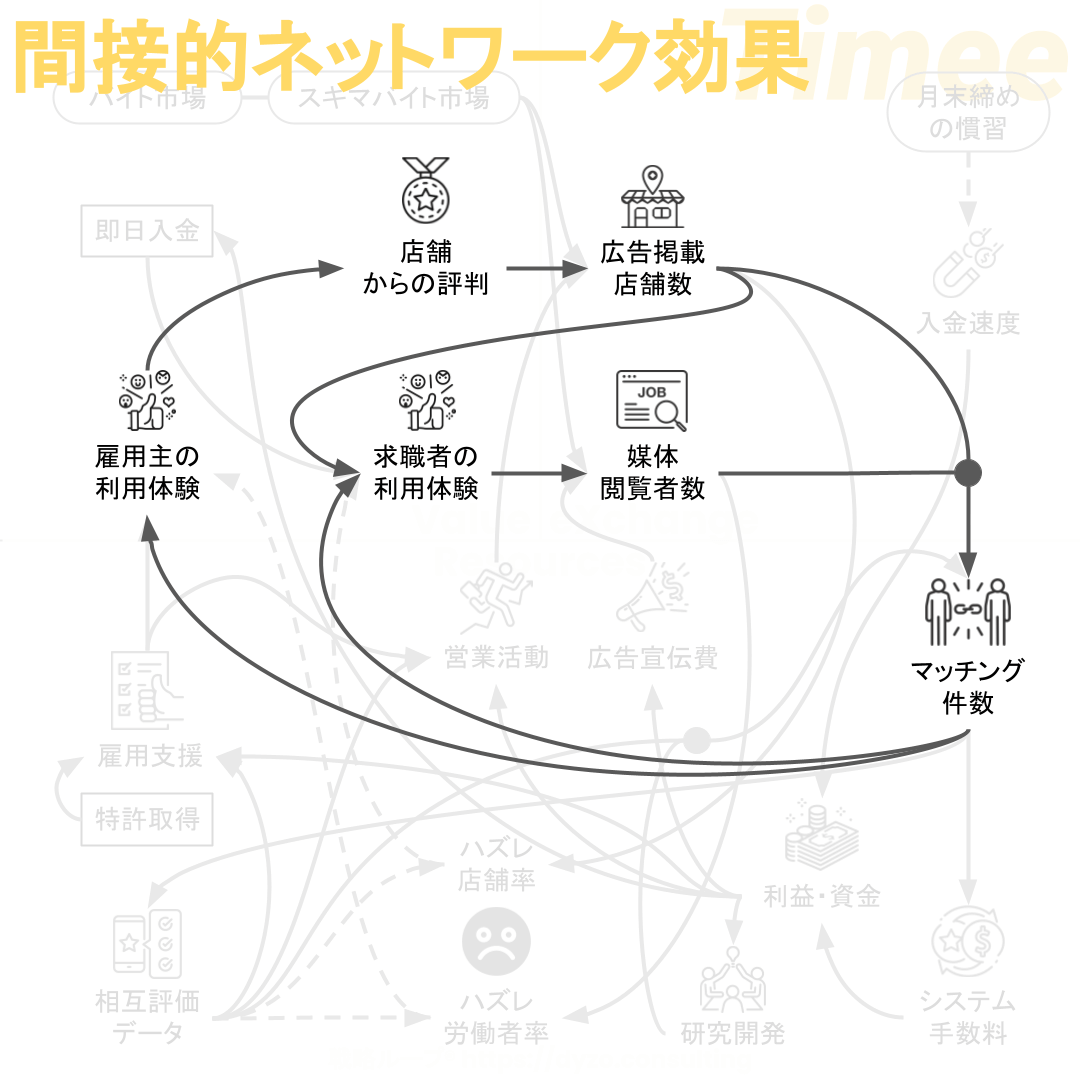
ネットワーク効果を得るためには、店舗数も求職者数も多いに越したことはありません。多ければ多いほど、利用者が利用者を呼ぶ状態になりやすくなります。
一気に広い範囲でサービスをスタートすれば、その分多くの利用者を獲得できるはず。
しかしタイミーは、逆に渋谷という非常に限定された地域でサービスをスタートさせました。
そのメリットは、
- 密度の経済性の活用
- クリティカルマスへの早期到達
の2つが考えられます。
タイミーが得た密度の経済性
密度の経済(Economies of density)とは、
- 人口密度の高い場所でビジネスを行うことで様々なコストを引き下げることができる
という考え方のこと。
特にサービス業においては、人口密度が2倍になるごとに生産性が10〜20%ほど向上するという研究結果もあります。
渋谷エリアは、タイミーが初期のターゲットである、
- 飲食店(店舗)
- 大学生(求職者)
が特に多く集まる地域のひとつであり、地の利を得るには最適な場所かと思います。
タイミーは渋谷エリアの密度の経済を活かすことで、効率よく飲食店に営業活動を行い、求職者である大学生の認知度を高めていったことが想像に難くありません。
さらに、顧客になった店舗にも細やかなサポートが必要になるため、対象エリアが狭い方が運営コストも抑えることができます。
このように、限られた創業当初のタイミーのメンバー数人で、できる限り多くの店舗と求職者をカバーするためには、渋谷エリアで密度の経済性の恩恵を受けることが最適だったと考えられます。
クリティカルマス(臨界質量)への早期到達
ネットワーク効果は、初めから現れることはありません。どんなビジネスも、初めはちょっとずつしか利用者が増えません。
利用者が利用者を呼ぶような状態になるためには、ある一定の利用者数を超える必要があります。
その「ある一定の利用者数」のことを、「クリティカル・マス(臨界質量)」と呼びます。
クリティカルマスは、ターゲット層ごとに存在しています。ターゲット層を小さくすればクリティカルマスも小さくなり、逆にターゲット層を大きく広げればクリティカルマスも大きくなります。(もちろん、クリティカルマスにも下限があるはずなので、どこまでも小さくすることはできませんが…。)
つまり、最初のターゲット層をある程度小さく設定していれば、クリティカルマスも小さくなり、必要な利用者の絶対数も小さくなります。そして、限られたターゲット層の中で、早期にネットワーク効果が働き始めるのです。
これは、創業当初のFacebookがサービス範囲をハーバード大学のみに限定していたことも同様です。Facebookは、まずはハーバード大学内のみでクリティカルマスを達成しました。
その後、スタンフォード大学、コロンビア大学、イエール大学と少しずつサービス範囲を広げながら、ネットワーク効果を維持し続けるように運営しました。(Facebookのエピソードについては、以下のページに詳しく書いているのでご覧ください。)
タイミーに置き換えて考えてみると、「渋谷エリア」はFacebookにとっての「ハーバード大学」ということです。
初期の市場を渋谷エリアに限定することで、クリティカルマスが「渋谷エリア内」かつ「スキマバイト」のみという、とても小さなものになります。
時系列で見ると、
- 2018年後半:渋谷エリアを中心に拡大
- 2019年前半:東京都を中心にエリアを拡大
- 2019年後半:首都圏、関西、福岡にエリアを拡大
- 2020年前半:東海、熊本にエリアを拡大
- 2021年前半:関東、関西、中京、福岡でCMを放映
- 2021年後半:東北エリアに拡大
という形で徐々にサービス範囲を広げていることがわかります。(プレスリリース等で拾った情報なので、抜け漏れがあればごめんなさい。)しかも、密度の経済性の効果が得やすい、人口密度の高いエリアを優先していることもわかります。
このように、タイミーは密度の経済性を得ながら、クリティカルマスをコントロールすることによって、初期の段階で失速することなく事業を成長させることができました。