NPV（正味現在価値）とは？計算方法とExcelの関数をわかりやすく図解

まず最初に「時間軸」を書き出して、その上下にお金の出入を図示しましょう。

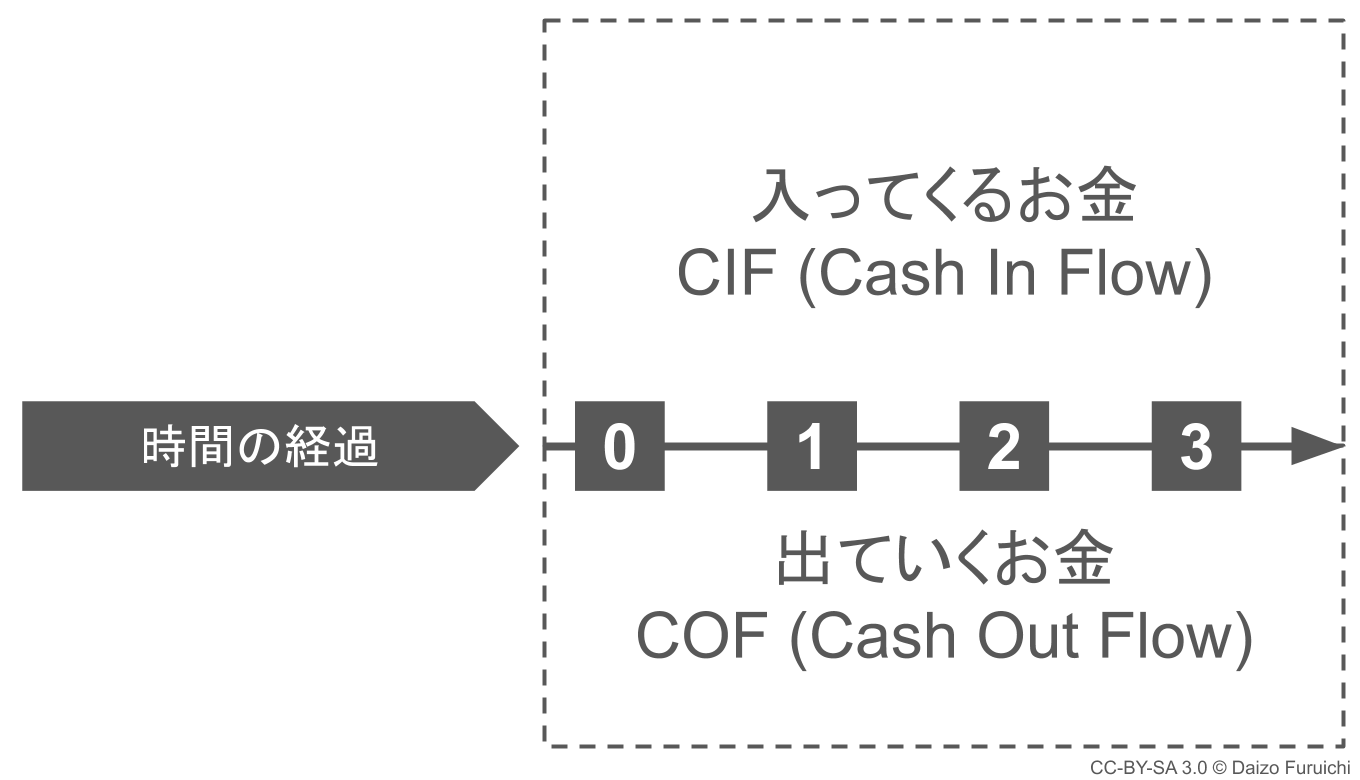
今回は現時点から3年後までを考えるので、0〜3年の時間軸の線を引きます。

そしてその線の上に「入ってくるお金」を書き、線の下に「出ていくお金」を書き込みます。

これらを書き込んでみると、このようになります。

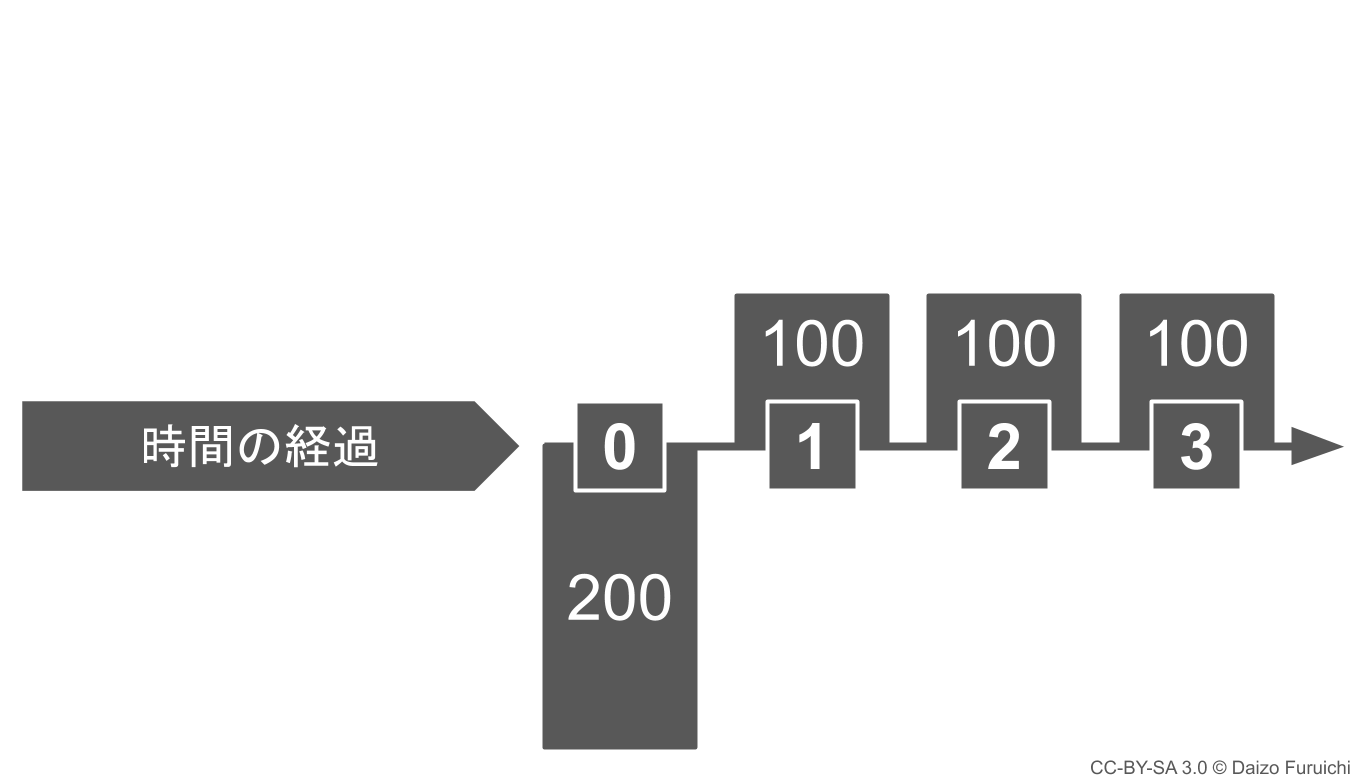
0年後（今）の初期投資額は200万円なので、200万円を下向きの棒グラフを書き込みます。そして1〜3年後はプラスなので上向きにの棒グラフで100万円を書き込みます。

しかし、このままでは初期投資額の200万円と、そのあと得られる300万円は単純に比較できません。

なぜなら目の前のお金と、将来もらえるお金は金額が同じでも価値に差があるからです。（理由は「現在価値とは？Excelでの計算方法と割引率をわかりやすく解説」の記事を参照）

この価値の差を埋めるためには、将来の金額を「現在価値」に揃える必要があります。

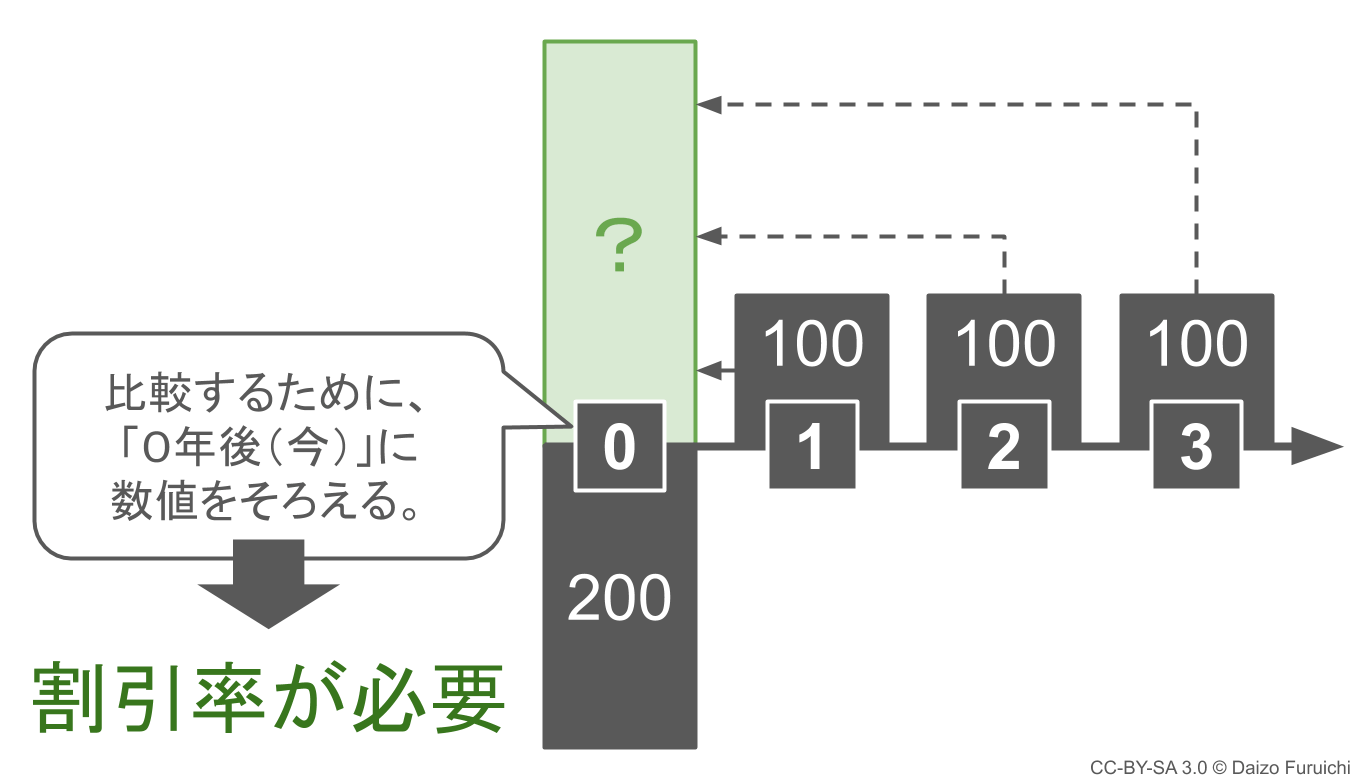
そして数字を揃えるためには「割引率」が必要になります。

ここでは、

• 割引率（r）：5%（0.05）

が与えられているので、これを使って計算します。

また現在価値の計算式は、

• 現在価値 ＝ N年後の金額 ÷ (1 + 割引率)^N

です。

1年後、2年後、3年後について、それぞれの現在価値を計算すると下図のようになります。

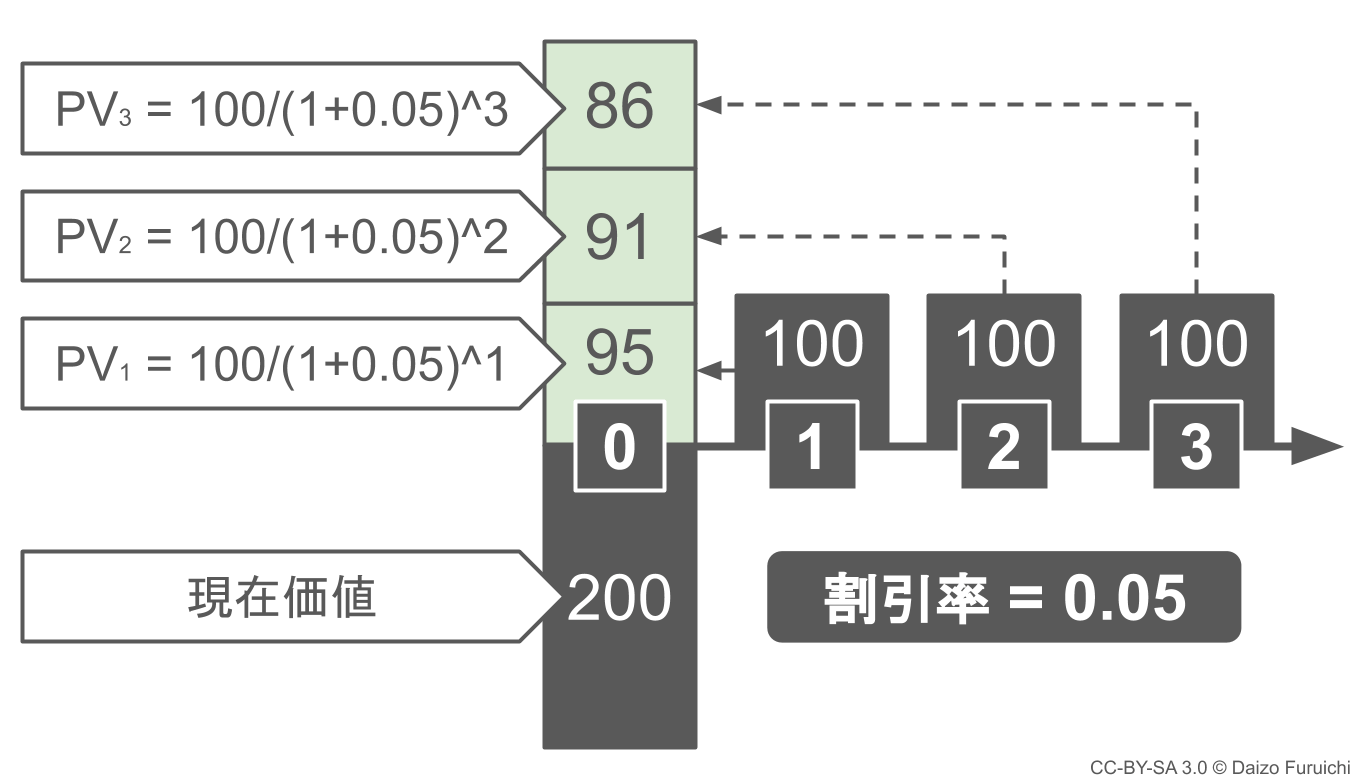
ちなみに今回の初期投資額は、すでに現在価値なので特に計算は必要ありません。（ただし、数年後に再投資や追加投資が必要な場合は、現在価値に割り引く必要があります。）

• 1年後の現在価値：100 ÷ (1+0.05)^1 = 95.2380…
• 2年後の現在価値：100 ÷ (1+0.05)^2 = 90.7029…
• 3年後の現在価値：100 ÷ (1+0.05)^3 = 86.3838…

ということで、これでやっと全ての数字が「現在（0年後）」にそろいました。

ここからは、現在の価値に直した数値をすべて合算します。

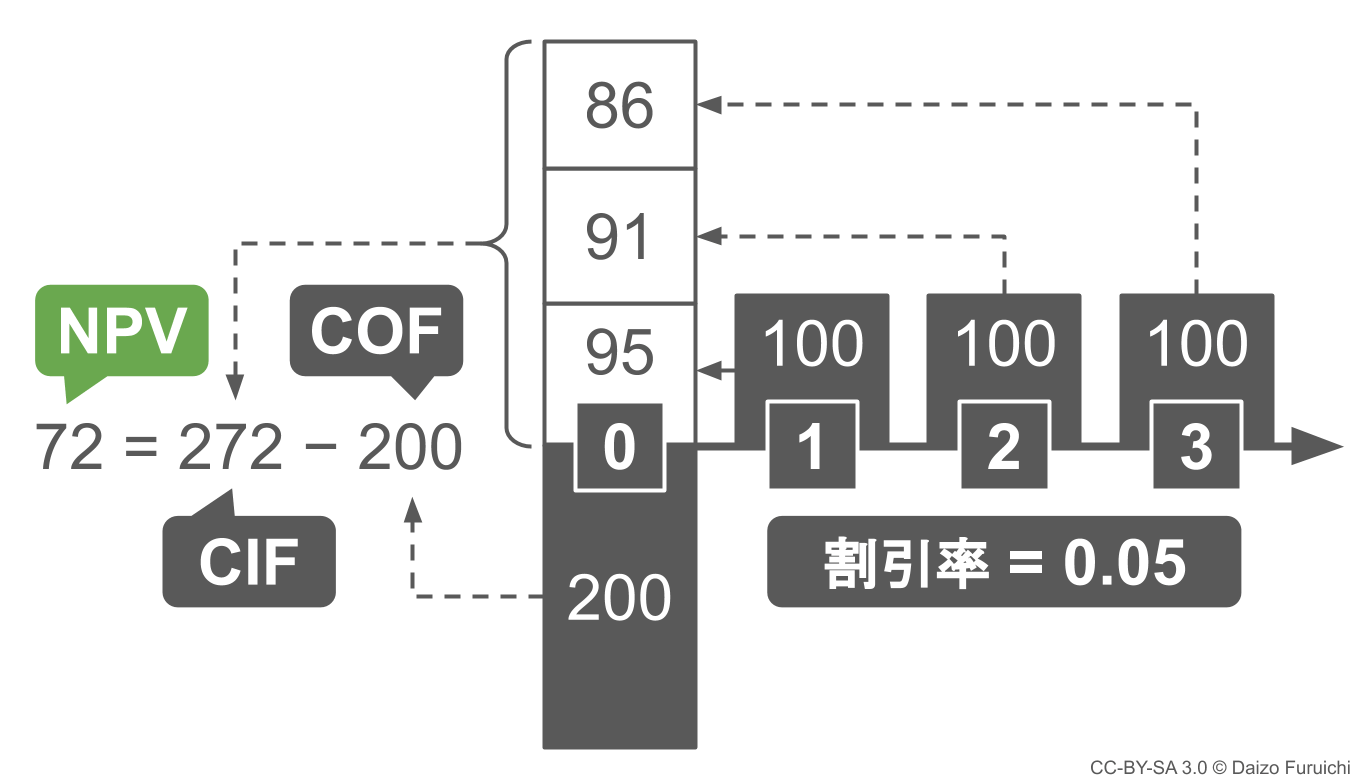
そうすると、

• CIF（キャッシュ・イン・フロー）：272万円
• COF（キャッシュ・アウト・フロー）：200万円

となって、

• NPV（正味現在価値）：72万円

という数値を導くことができました。