だいぞう
だいぞう
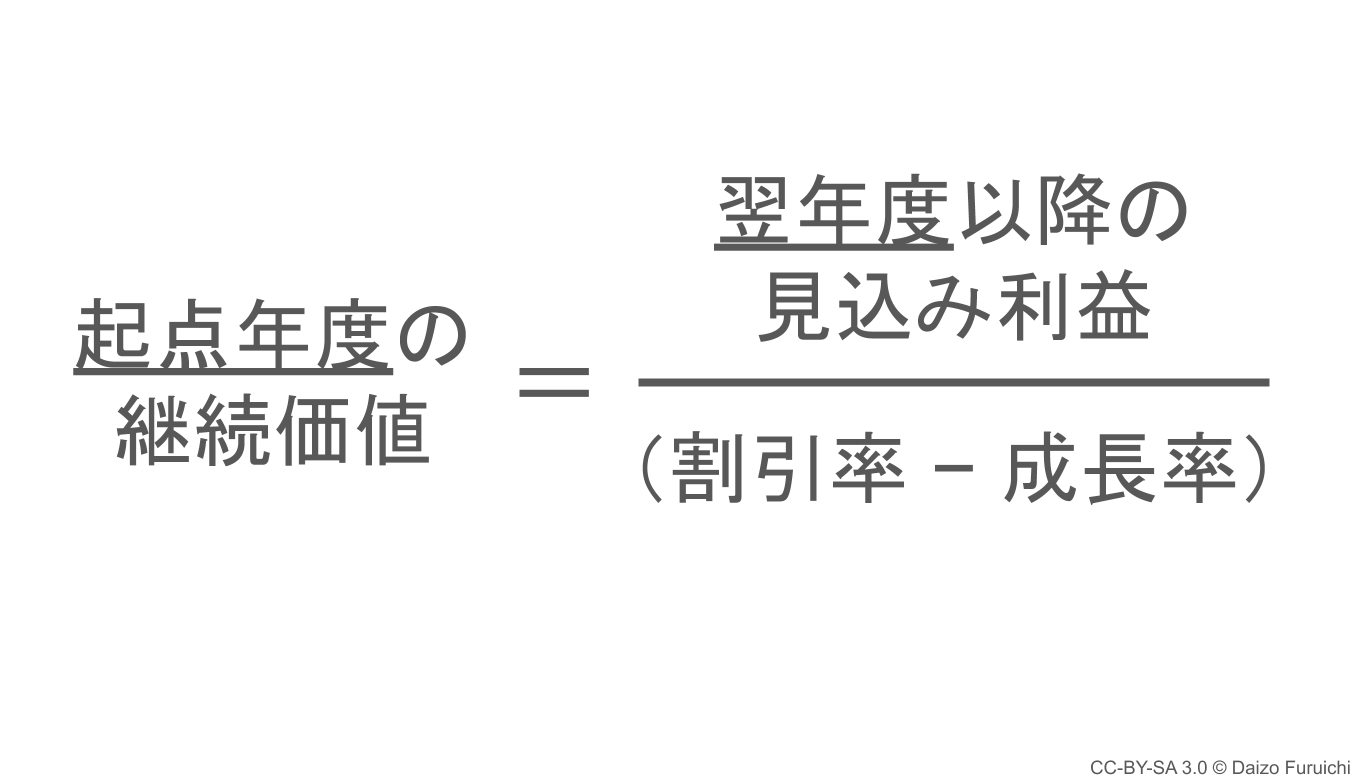
ターミナルバリュー(Terminal Value)とは、
- 安定した事業成長が永遠に続くと仮定した場合のキャッシュフロー合計の現在価値
のことで、「継続価値」「永続価値」「残存価値」「最終価値」などとも呼ばれます。
企業価値を計算する場合や、将来の予測が難しいプロジェクトの現在価値を計算する場合に用いられます。
ターミナルバリューを計算するためには、
- 割引率
- 成長率(永久成長率)
を設定する必要があり、公式は下記のようになります。
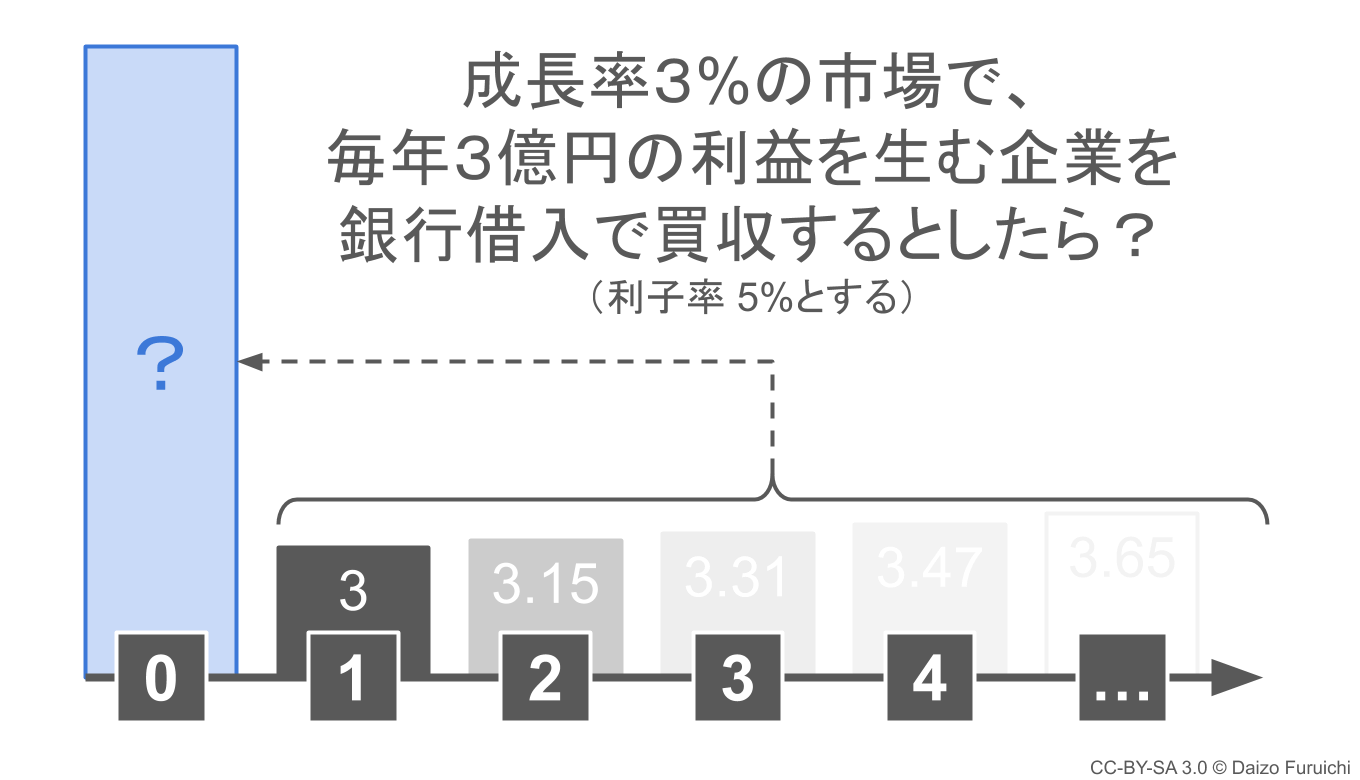
具体例として、
- 毎年安定的に3億円の利益を生み出している企業がある
- その企業が参入している市場の成長率は3%
- 銀行からの借り入れ(利子率5%)でその企業を買収する
といった場合を想定して計算をしてみます。
この設定から得られた条件を整理すると、
- 毎年のキャッシュフロー:3(億円)
- 割引率(利子率):5%
- 成長率(永久成長率):3%
ということになります。
これを計算すると下図のようになります。
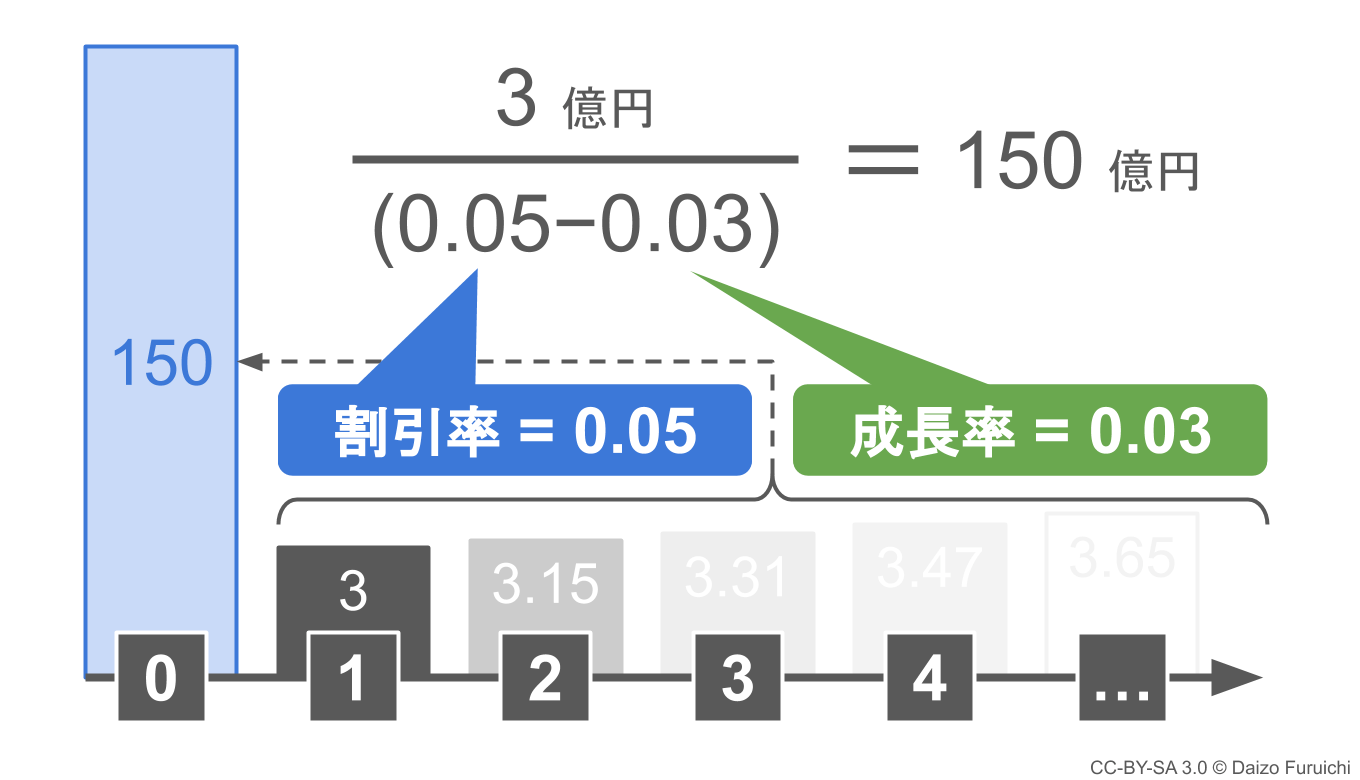
ということで計算結果は、
- 3 ÷ (0.05 – 0.03) = 150
になり、その企業を買収する目安の金額は150億円ということになります。また、150億円よりも低い金額で買うことができれば「お得な買い物」と言えます。
(※ここでの企業価値の計算はデューデリジェンスを目的としたものではなく、あくまでターミナルバリューの計算をわかりやすく説明するための題材として取り上げたものとしてご理解ください。)
ここではターミナルバリュー(継続価値)の計算について、わかりやすく説明します。