ターミナルバリューの計算式
ターミナルバリュー（継続価値）は冒頭でご紹介した通り、
- 起点年度の継続価値 ＝ 翌年度以降の見込み利益 ÷（割引率 ー 成長率）
で計算することができます。
もし「現在価値」や「割引率」という言葉にピンとこなければ、まずは以下の記事をご覧ください。
現在価値とは？Excelでの計算方法と割引率をわかりやすく解説
ということで、現在価値の計算の面倒さを知っていると、
…と疑問がわく人もいるかもしれません。
例えば５年分の現在価値を計算しようと思えば、
- １年後の現在価値 ＝ １年後のキャッシュフロー ÷（１＋割引率）^１
- ２年後の現在価値 ＝ １年後のキャッシュフロー ÷（１＋割引率）^２
- ３年後の現在価値 ＝ １年後のキャッシュフロー ÷（１＋割引率）^３
- ４年後の現在価値 ＝ １年後のキャッシュフロー ÷（１＋割引率）^４
- ５年後の現在価値 ＝ １年後のキャッシュフロー ÷（１＋割引率）^５
と計算して、全てを合計する必要があります。
もし10年分なら10回計算する必要がありますし、100年だったら100回計算しなければならないかもしれません。ましてや永続価値なら何回計算するのか途方に暮れてしまいます。
しかしそんな面倒な作業も永続価値（ターミナルバリュー）については、
- 起点年度の継続価値 ＝ 翌年度以降の見込み利益 ÷（割引率 ー 成長率）
という１つのシンプルな公式で計算できてしまうのです。
これって、とても怪しい感じがしませんか？
ということで計算してみました！
エクセルで継続価値の計算結果を比較
ここでのターミナルバリューの計算は、
- 毎年のキャッシュフロー：100
- 割引率：50%（0.5）
- 成長率：3%（0.03）
という条件を設定してます。
とりあえず20期分を計算して比較してみました。（※20期で近似値を比較するために、割引率を高く設定してます。）
そして計算結果が以下の通り。（※数値は小数点第四位で四捨五入）
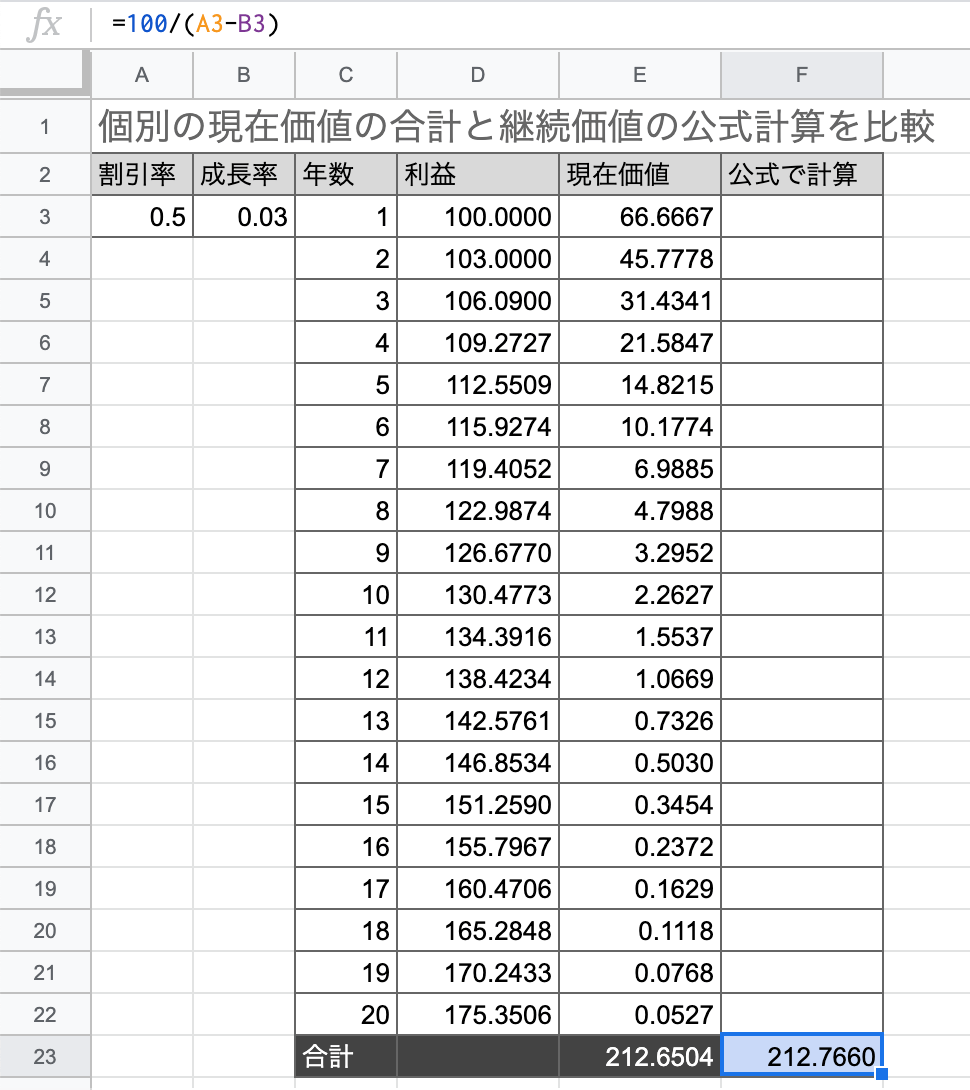
セル「E23」が、毎年3%ずつ成長する利益の現在価値を20年分計算したものの合計値になります。そして、その隣のセル「F23」が、「100」「0.5」「0.03」というたった３つの数字を使っただけの数値です。
比較すると、
- 個別の現在価値の合計値：212.6504…
- 公式を使った永続価値：212.7660…
という数字になりました。
いかがでしょうか？ ２つの計算方法の結果がほぼ同じ数値です。
もし個別の現在価値の計算をあと何十年分か行えば、公式を使って計算したターミナルバリューの数値にさらに近づくはずです。
継続価値は起点年度の現在価値
ターミナルバリュー（継続価値）で注意しなければならないのは、
- 計算結果が「起点」とする年度に割り戻した現在価値になる
ということです。
例えば、
- 4年後以降のキャッシュフローが毎年同じ
という条件設定であれば、ターミナルバリューの計算結果は、
- 3年後の時点に割り戻した現在価値
になります。
つまり「現時点」での現在価値を計算する場合は、
- ３年後の時点の現在価値をさらに３年割り戻す計算
が必要になります。
この計算については、後述する具体例でも説明します。
