ターミナルバリューの計算方法:CFが一定の場合
まずは一番シンプルな、毎年のキャッシュフローが成長せずに一定である場合のターミナルバリューの計算を確認します。
ここでは単純なターミナルバリューの計算だけでなく「新規事業」として、初期投資を行う想定で、NPV(正味現在価値)を考えてみたいと思います。
ちなみに以前のNPVの記事では例題として、
- 初期投資額:200万円
- 1年後から3年間生まれる利益:100万円
- 割引率:5%(0.05)
という設定で計算しました。
その結果が下記の図になります。(※計算結果は小数点以下を四捨五入)
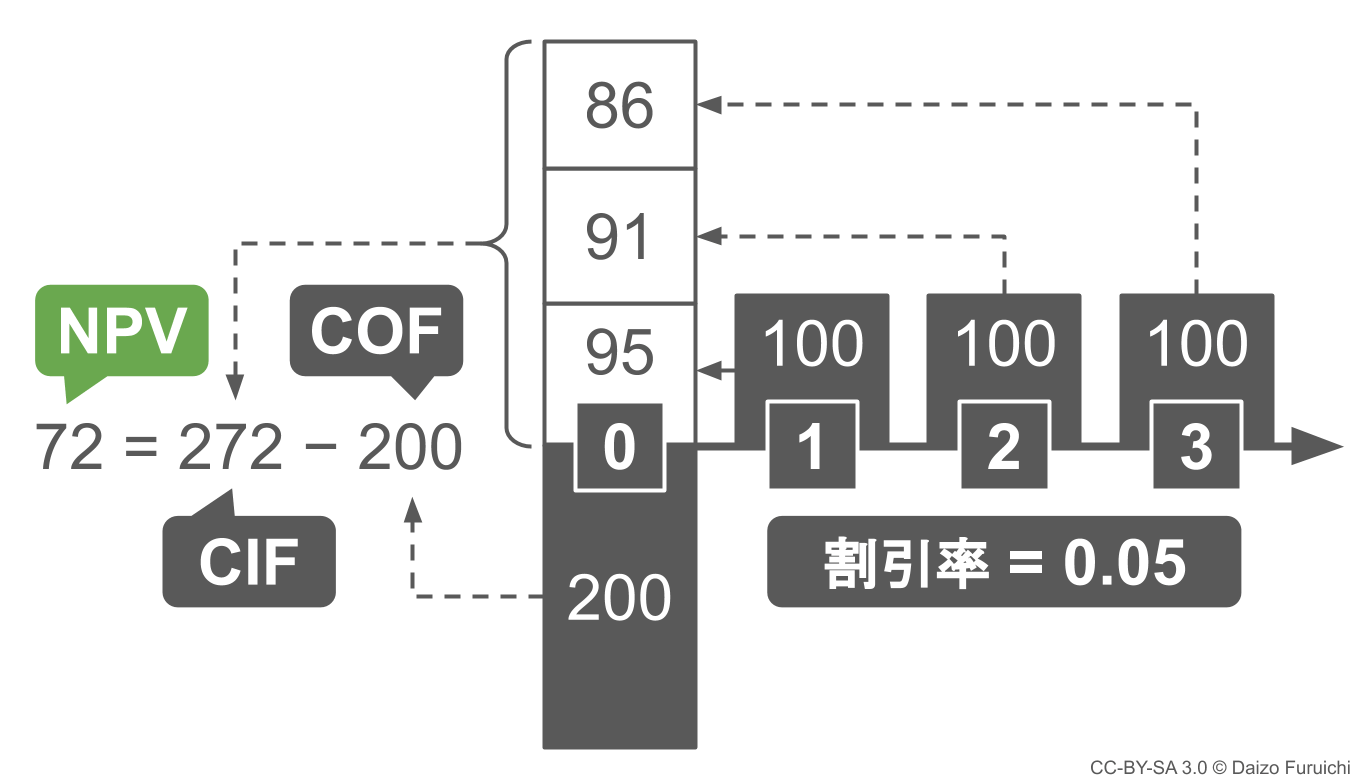
このNPVの例題では、キャッシュフローが生まれる期間を3年間に限定しています。
しかし今回のターミナルバリューの例題では、キャッシュフローが永遠に生まれるという想定で計算します。
ということで条件を、
- 初期投資額:200万円
- 毎年のキャッシュフロー:100万円
- 割引率:5%(0.05)
- 成長率:なし
としてNPV(正味現在価値)の計算を図に表すと、下記のようになります。
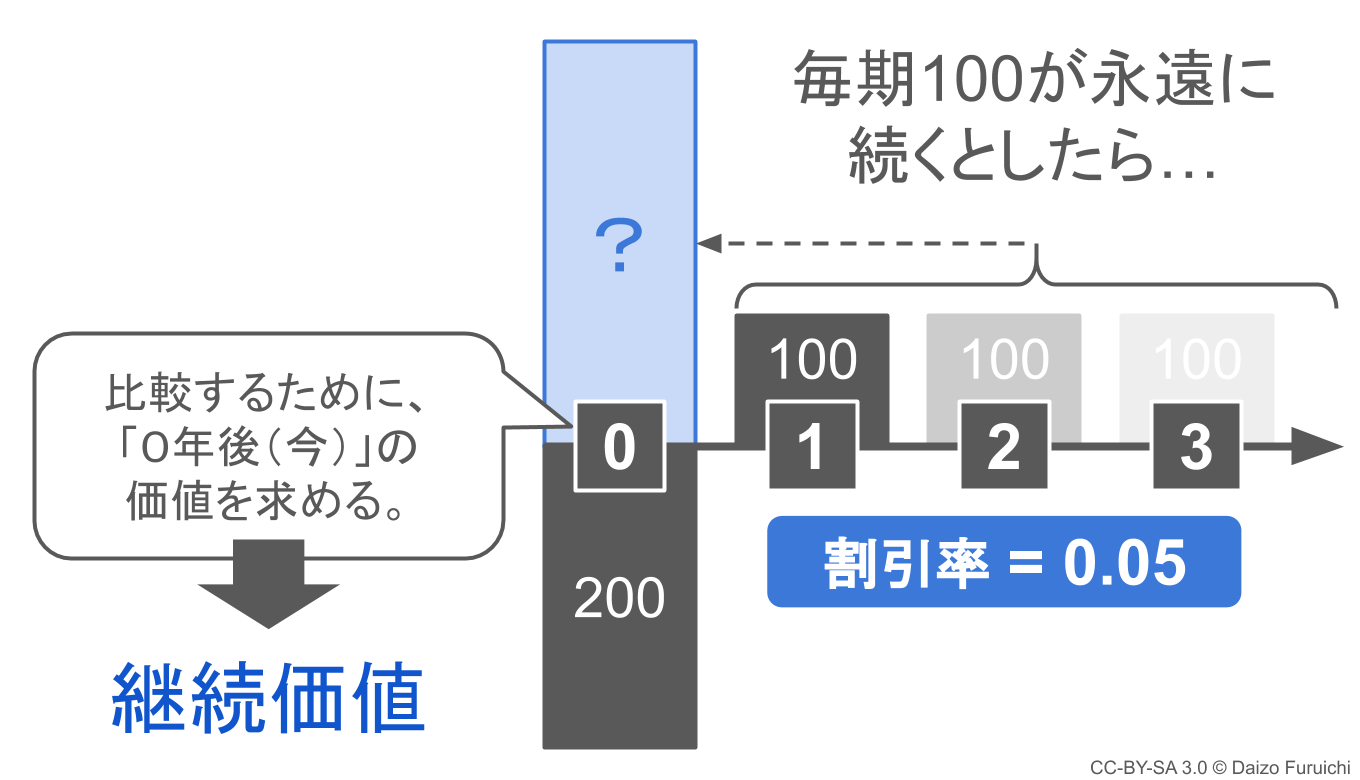
1年後以降のキャッシュフローの合計値を、初期投資額と計算するためには、継続的なキャッシュフローの「継続価値(ターミナルバリュー)」を求めなければなりません。
ということで、こちらのターミナルバリューの計算式を使います。

今回はキャッシュフローが「一定」ということなので、
- 成長率 = 0
で計算します。
そうするとターミナルバリューの計算式は、
- TV = 100 ÷ 0.05
となります。
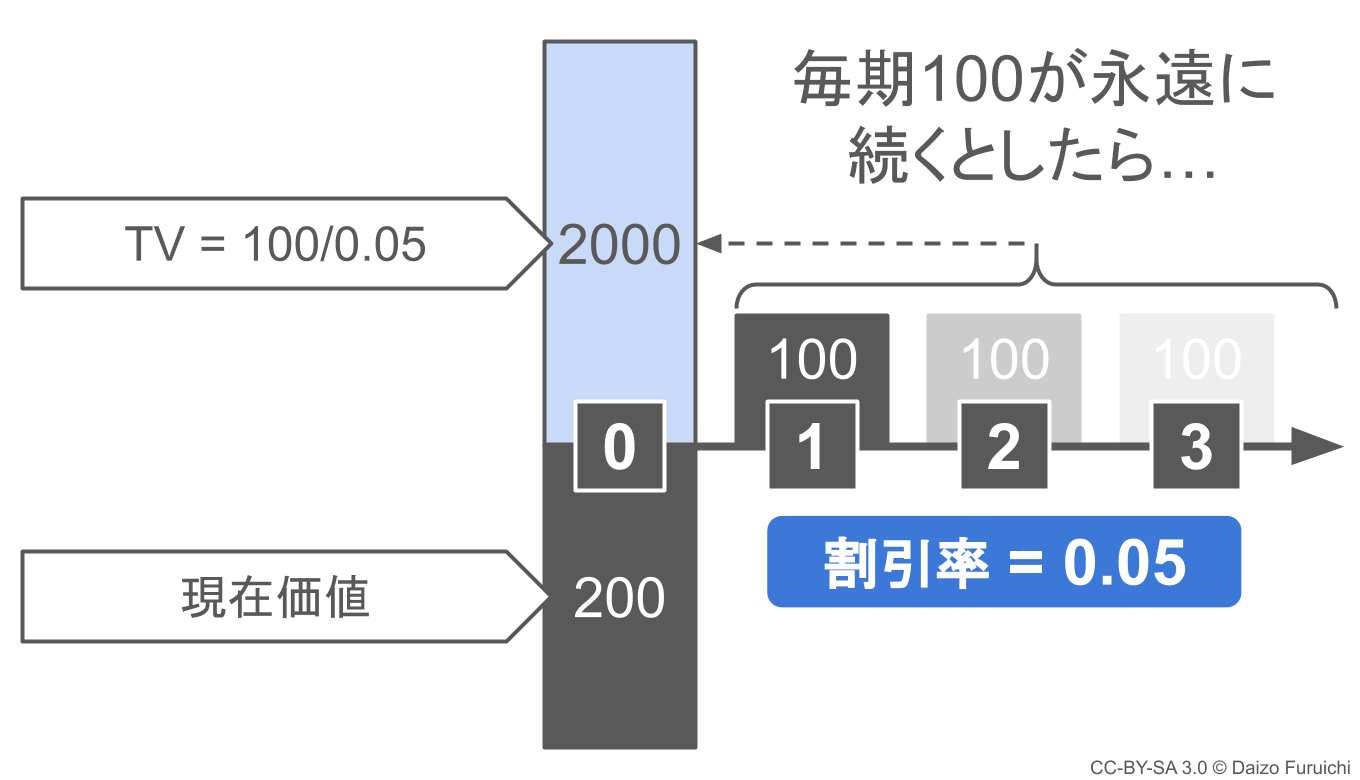
この結果、
- ターミナルバリュー = 2000
ということがわかりました。
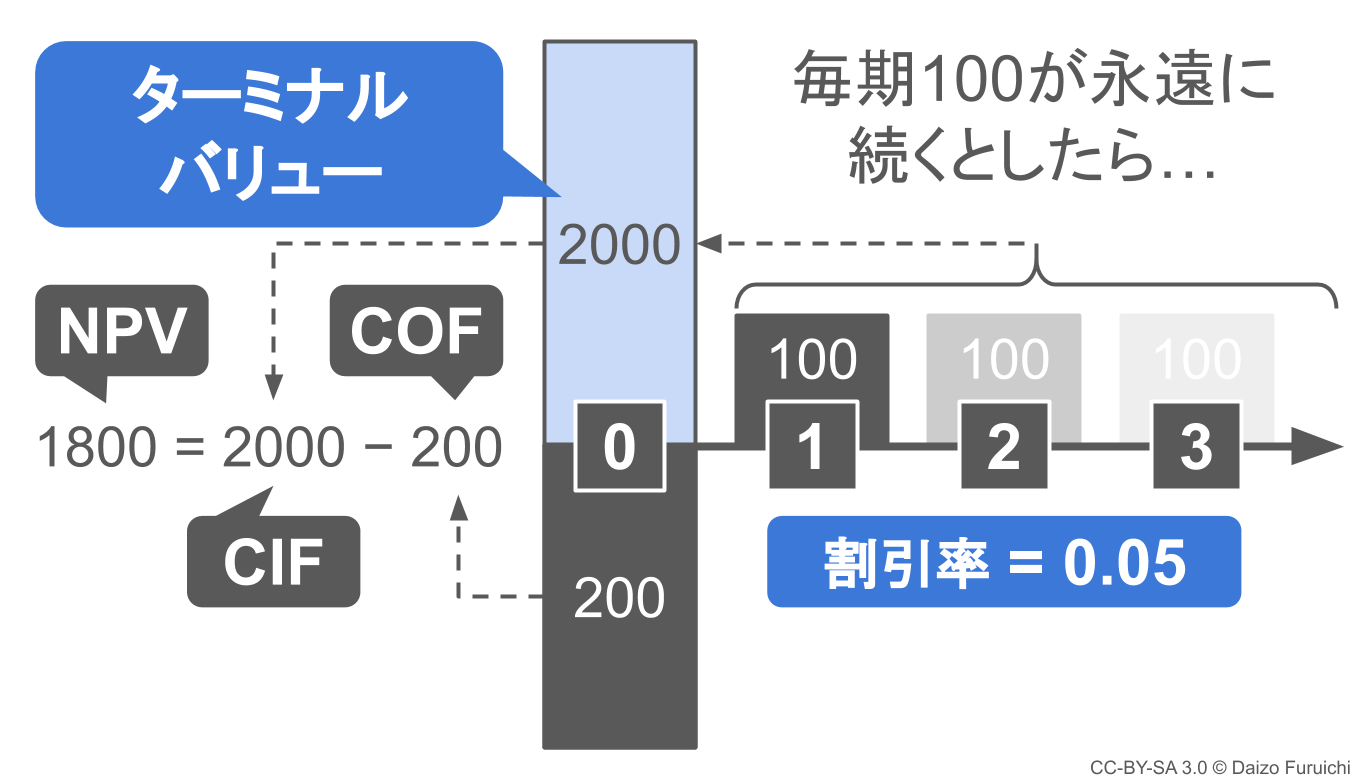
このターミナルバリューは「0年後(現時点)」のものなので、初期投資額を差し引くことでNPV(正味現在価値)を計算することができます。