粗利率(売上高総利益率)の分析パターン
粗利率を分析した結果は、
- 売上高がほぼ同じなのに粗利率に差が出るパターン
- 売上原価がほぼ同じなのに粗利率に差が出るパターン
- 粗利(売上総利益)がほぼ同じなのに粗利率に差が出るパターン
という3つのパターンに分けることができます。
またそれぞれのパターンは、
- 期間比較分析:今年度と前年度のように同じ長さの期間で比較する
- 相互比較分析:自社と競合他社のように複数社間で比較する
- 標準比較分析:自社と業界平均のように標準となる数値と比較する
などの分析方法から導かれます。
なお、ここでは「期間比較」と「相互比較」を中心に解説を行います。
補足
「標準比較」の分析は、何を「標準」とするかを決めるのが非常に難しい分析方法です。
仮に「業界平均」を標準として比較をしようとしても、
- 上位の企業が平均値を引き揚げてしまい参考にならないことがある
- 業績が二極化するような業界では「平均的」な企業が存在しない場合がある
- 同じ業界内でもビジネスモデルが異なると平均をとる意味がない
- どこまでの範囲を「業界」に含めるかのさじ加減で平均値が変わってしまう
などといった理由で「平均値」が使い物にならないことがあります。
そのため「標準比較」を行う場合には、上記の点に気をつける必要があります。
売上高がほぼ同じなのに粗利率に差が出るパターン
売上高が同じであれば、
- 売上原価が大きい → 売上総利益(粗利)が小さくなる → 売上高総利益率が低い
- 売上原価が小さい → 売上総利益(粗利)が大きくなる → 売上高総利益率が高い
ということになります。
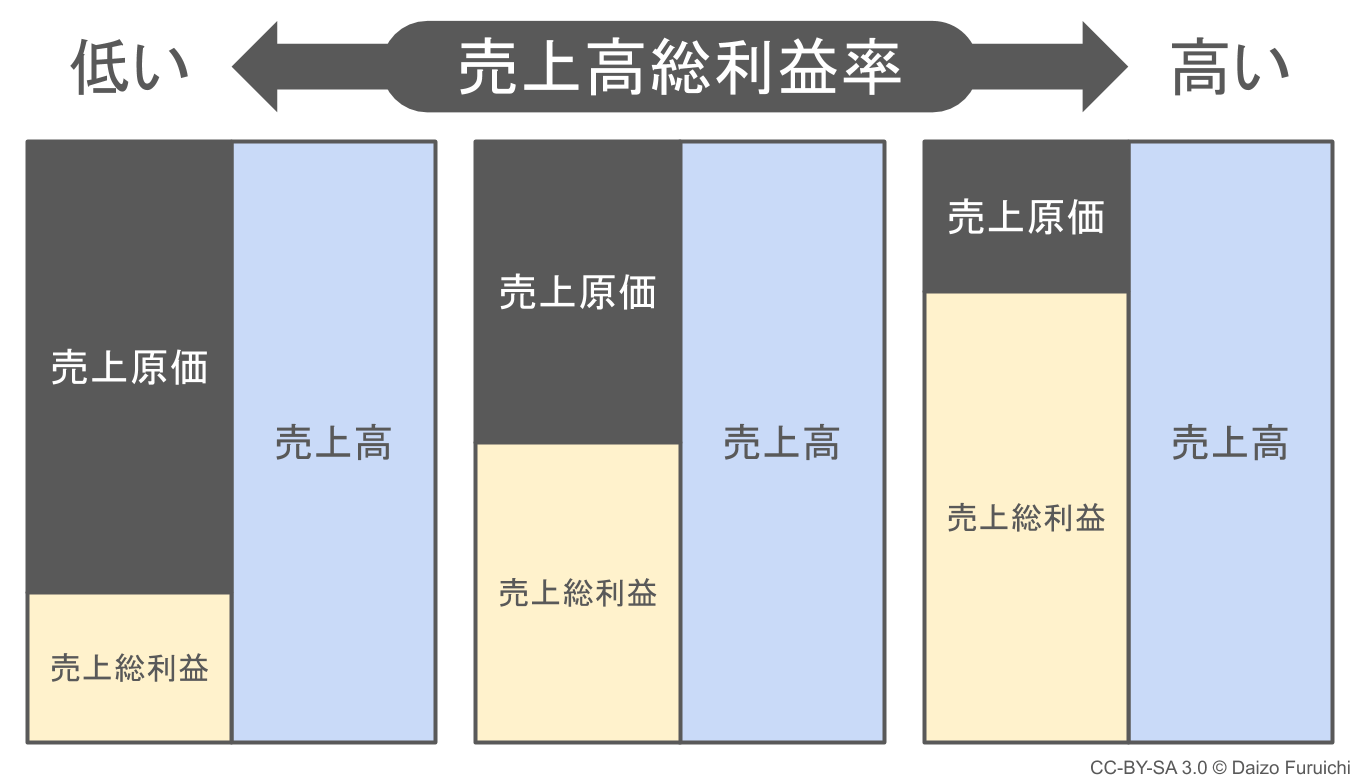
売上高が同じ場合には、売上原価の割合の差によって売上高総利益率(粗利率)に違いが生まれます。
売上原価がほぼ同じなのに粗利率に差が出るパターン
売上原価が同じであれば、
- 売上高が小さい → 売上総利益(粗利)も小さくなる → 売上高総利益率が低い
- 売上高が大きい → 売上総利益(粗利)も大きくなる → 売上高総利益率が高い
ということになります。
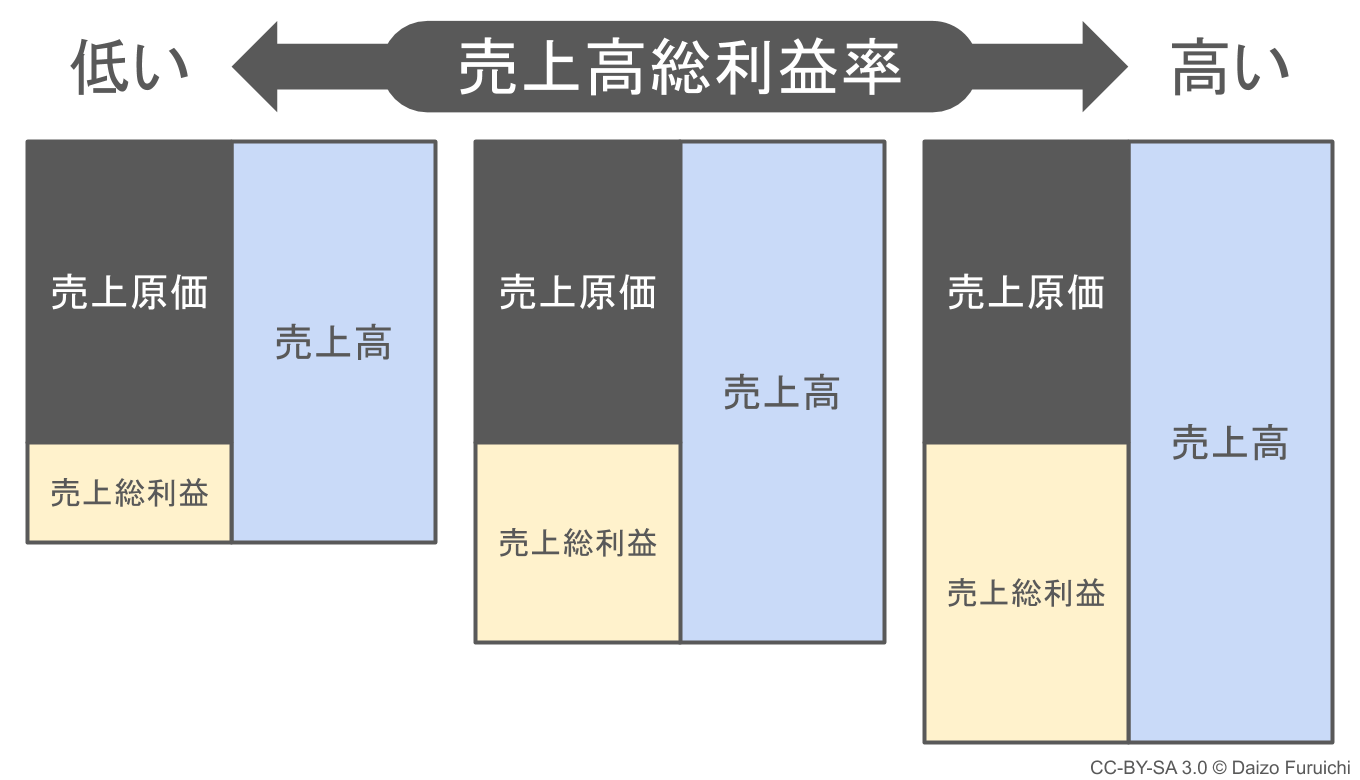
かかるコスト(売上原価)が同じ場合には、売上規模の差によって売上高総利益率(粗利率)に違いが生まれます。
粗利(売上総利益)がほぼ同じなのに粗利率に差が出るパターン
粗利(売上総利益)が同じであれば、
- 売上高が大きい → 売上原価も大きくなる → 売上高総利益率が低い
- 売上高が小さい → 売上原価も小さくなる → 売上高総利益率が高い
ということになります。
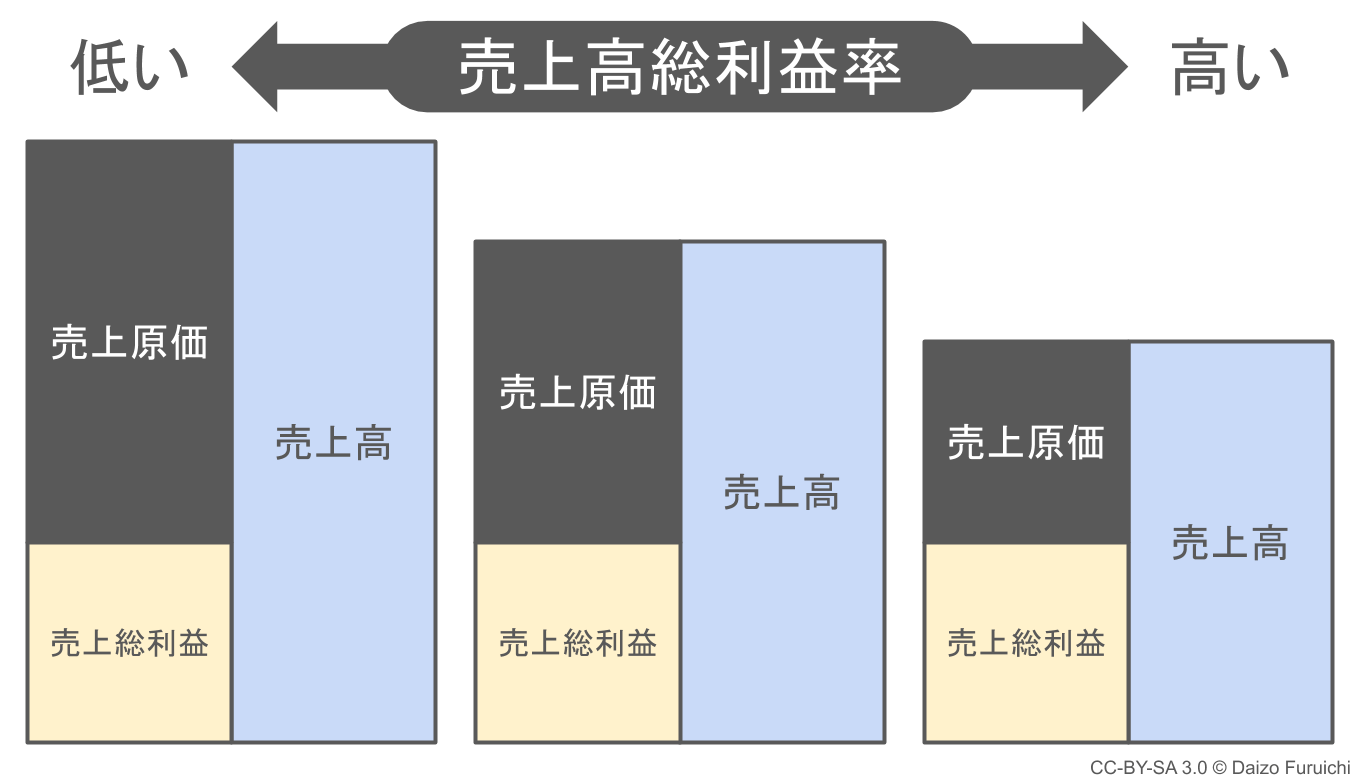
売上総利益(粗利)が同じであれば、売上規模の差によって売上高総利益率(粗利率)に違いが生まれます。