だいぞう
だいぞう
パレートの法則とは、
- 大部分(80%)は全体の要素の一部(20%)で構成されているという経験則
のことで、「80対20の法則」「80:20の法則」「8:2の法則」「80/20の法則」などとも呼ばれます。
下図のような「べき乗則」のグラフで表現されることがほとんどです。
ビジネスの場面で使われるパレートの法則では、
- 製品の20%が売上の80%を稼いでいる
- 2割のお得意様が会社の利益の8割をもたらしてくれる
などが代表的なものになります。
ここでは「パレートの法則(80対20の法則)」に加えて「ロングテール」「働きアリの法則(2-6-2の法則)」などについても、図を交えてわかりやすく説明します。
パレートの法則(80対20の法則)とは?
パレートの法則(80対20の法則)とは、1896年にイタリアの経済学者であるヴィルフレド・パレート(Vilfredo Pareto)氏の研究で、
- イタリアの国土の80%は人口の20%によって所有されている
という研究結果が導かれたことに由来しています。
この法則は近年でも、
- 世界の上位20%のお金持ちが世界の所得の82.7%をコントロールしている(Human Development Report, New York: Oxford University Press 1992年 )
- アメリカの上位20%のお金持ちがアメリカの税金の87%を支払っている(米ウォール・ストリート・ジャーナル「Top 20% of Americans Will Pay 87% of Income Tax」2018年 )
という研究結果が得られていて、富の分配という点において有効である事が確認されています。
べき乗則
このパレートの法則は、「べき乗則」のグラフがベースになっています。
べき乗則(冪乗則、Power law)とは、下図のようなグラフで表現される「統計モデル」の一種です。

このべき乗則というモデルでは、自然現象をはじめとして様々な事柄を説明できるモデルとして知られています。多くの事柄(グラフの上方向)が全体の一部(グラフの左部分)によって引き起こされていることが、グラフによって表されています。
そしてパレート氏がイタリア国内の富(土地の所有)の分配を研究した結果も、この「べき乗則」に従っている事がわかり、パレートの法則(80対20の法則)として多くの人に知られるようになりました。
パレートの法則の具体例
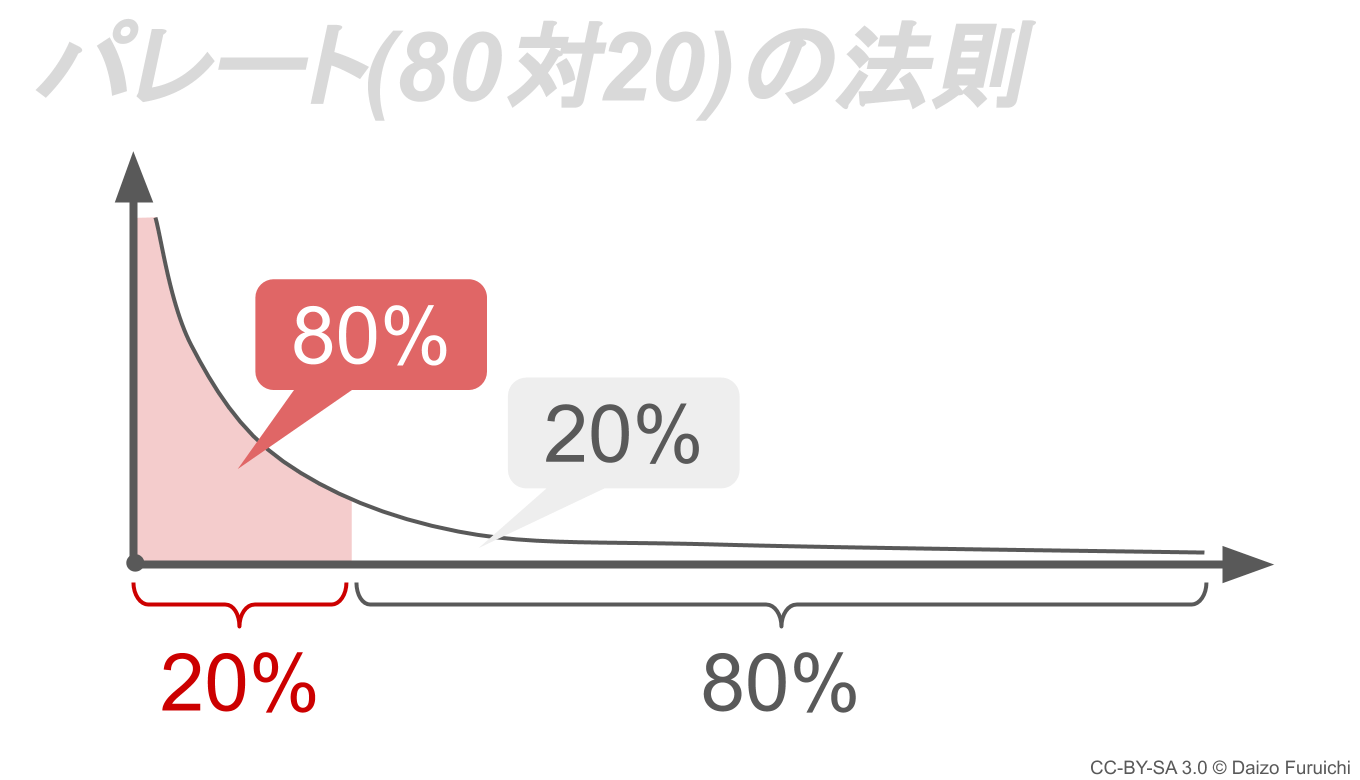
先ほどご紹介した「べき乗則」を使って、パレートの法則を表現すると下図のようになります。

パレート氏の富の配分の研究であれば、
- 縦軸:所有する土地の面積
- 横軸:所有する土地の面積順で左から並べた個人
ということになり、左から広い土地を所有する順で個人を並べ替えると、先頭の約20%の個人がイタリア国土の約80%(ピンク色の部分)を所有している事がわかります。
この「80対20」という割合が「80対20の法則」と呼ばれる理由でもありますが、現在では「一部ものもが大部分をもたらしている」という「経験則」として使われるようになりました。
そのため「80対20の法則」と言っても、必ずしも80対20の割合である必要はありません。
パレートの法則の具体例としては、
- 製品の20%が売上の80%を稼いでいる
- 2割のお得意様が会社の利益の8割をもたらしてくれる
- 2割の従業員が会社の売上の8割を生み出している
- 2割のプログラムの不具合を直せばエラーの8割が解決する
- ソフトウェアの機能の8割は2割のブログラムコードで動いている
- 自然災害の20%が自然災害被害者の80%を生んでいる
などなど、様々なものがあります。