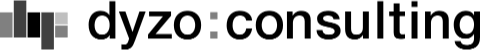システム思考のループ図:拡張ループを均衡させる要素
さて、先程の拡張ループを抑制する要素は何でしょうか?
1つの例を挙げるとすれば、「勉強しない生徒」の数です。
予備校の評判が良くなってくると、「自分もあの予備校に行けば合格できるのでは?」と期待する人も増えます。
もちろんみんな真面目に勉強してくれれば良いのですが、そうとは限りません。
極端な話「自分は勉強が苦手だけど、合格者の多いあの予備校に行けば、そんなに勉強しなくても合格できるかも?」と考える人も、どんどん入学してくるようになります。
このような状態を、経営学では「アドバース・セレクション(adverse selection:逆淘汰・逆選択)」と呼んだりします。
参考
ビジネスで考えるべき「アドバース・セレクション」とは何かダイヤモンドオンライン
いくら他人が合格しているからと言っても、資格試験で合格できるかどうかは本人の行動次第。しかし、勘違いをして入学してくる人も増えるのです。
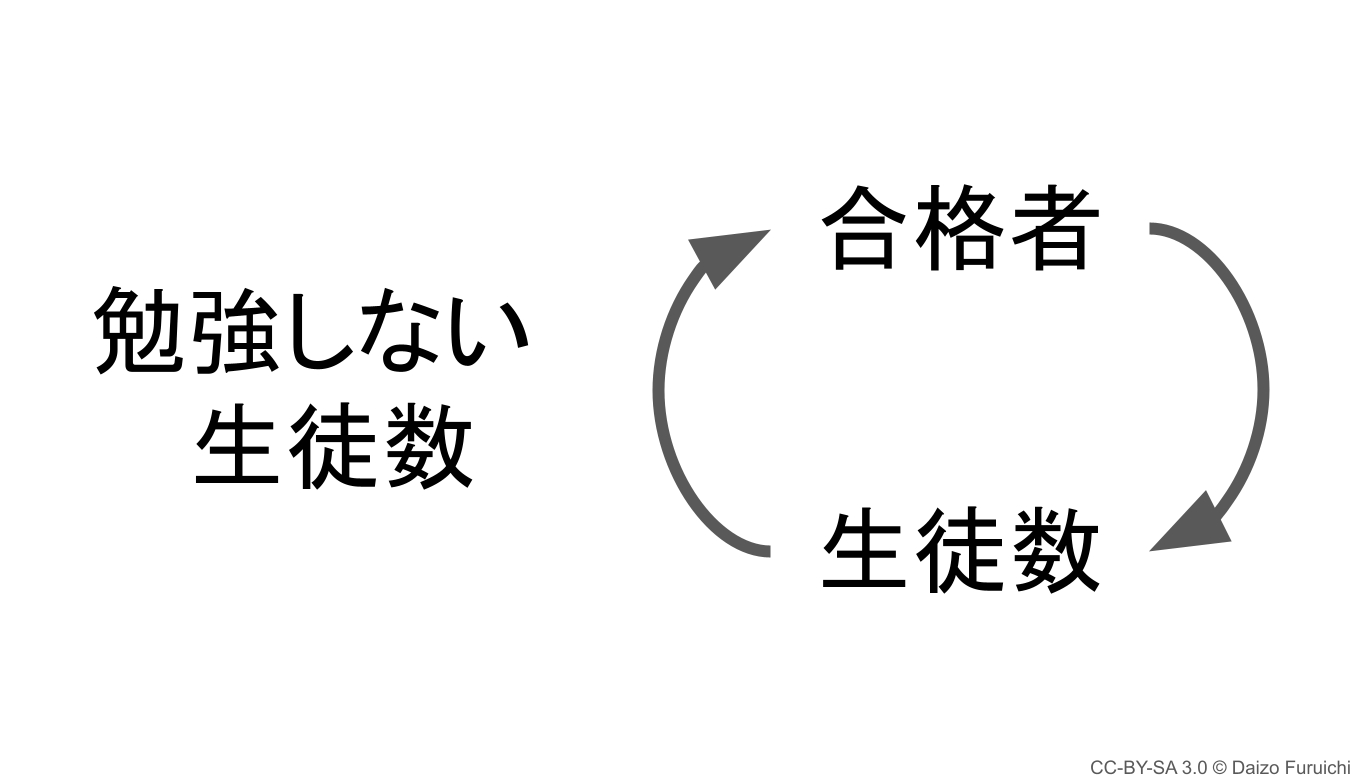
ループ図:生徒数から勉強しない生徒数へ伸びる矢印
これをループ図で表すと以下のとおり。
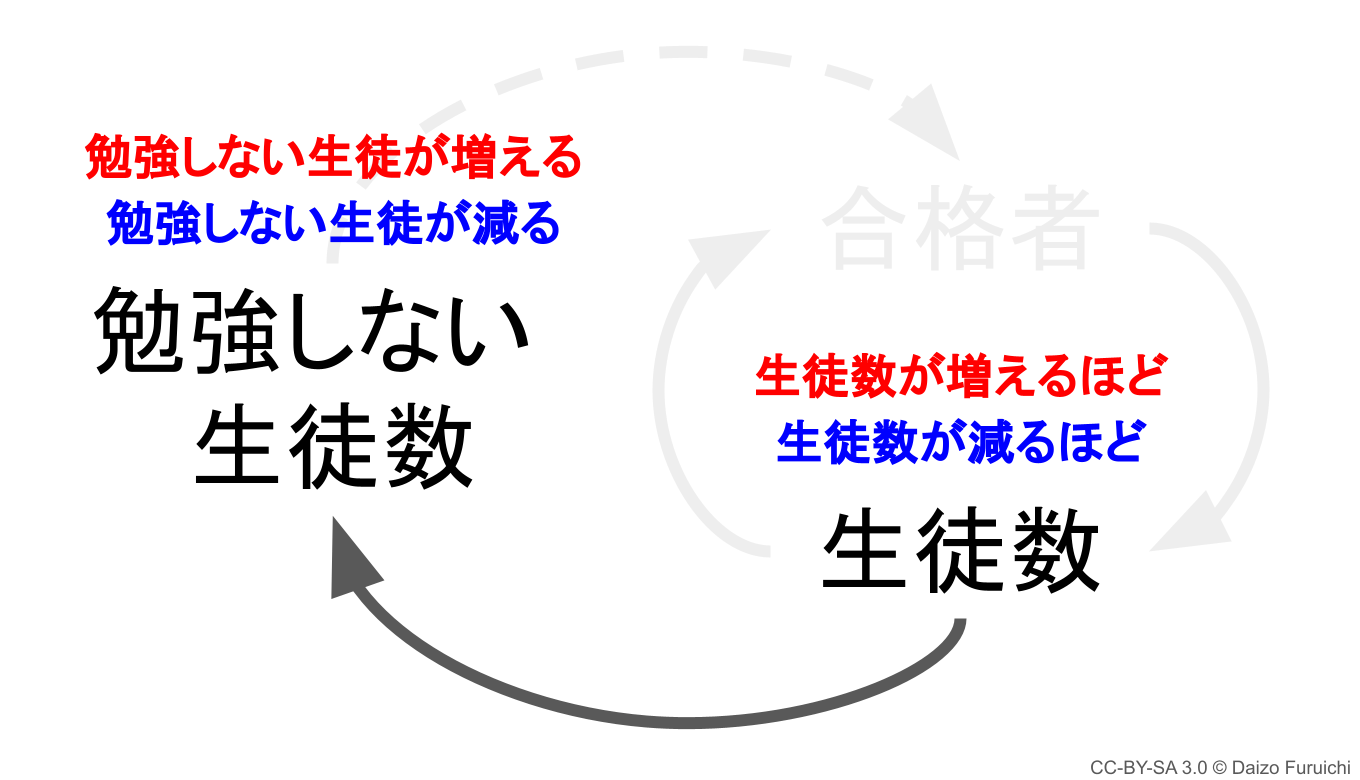
ここでの矢印は、
- 「生徒数」が増えるほど「勉強しない生徒」が増える
- 「生徒数」が減るほど「勉強しない生徒」が減る
という2つのパターンが存在することを表しています。
ループ図:勉強しない生徒数から合格者に伸びる矢印
さらに次がどうなるかというと…
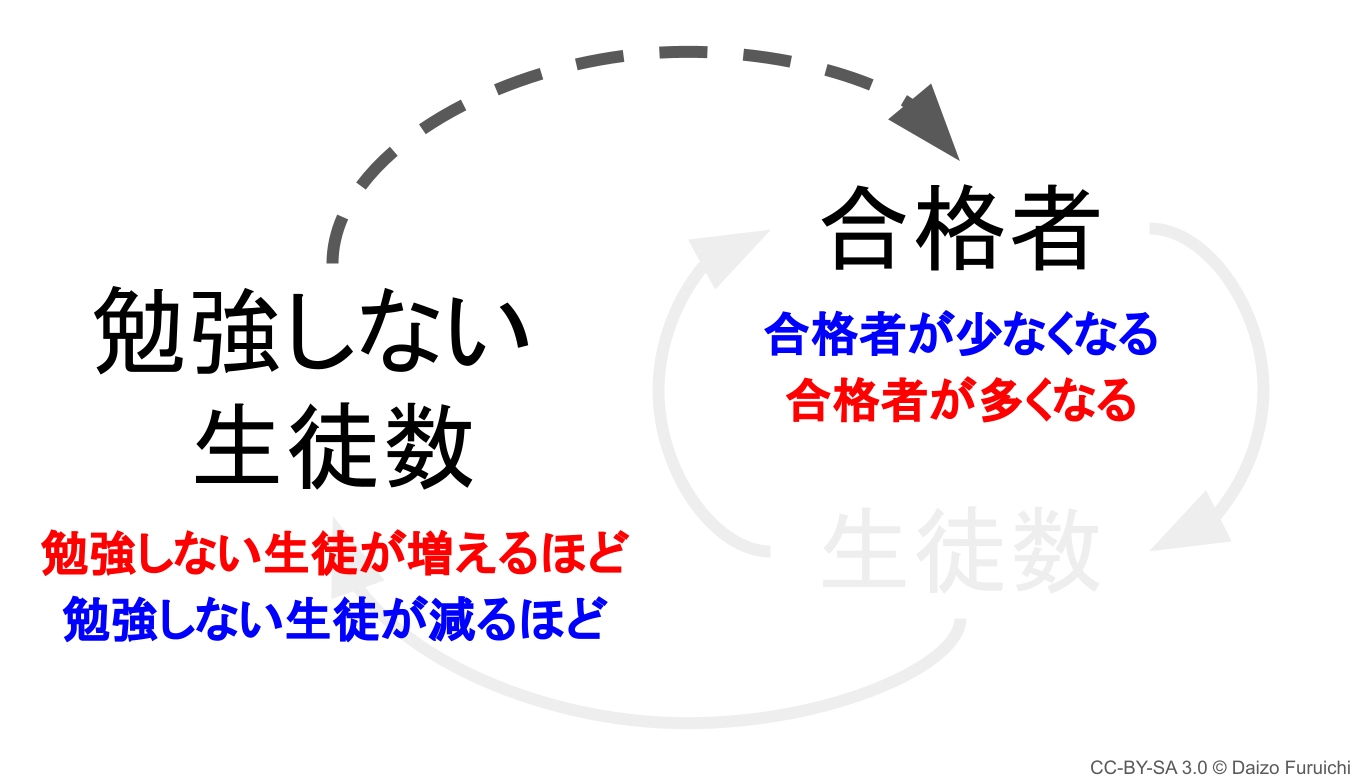
…合格者の数に影響してくるわけです。
ここで注意が必要! いままでとは違って、矢印が破線(点線)で表現されています。
つまりこの矢印は、
- 「勉強しない生徒」が増えるほど「合格者」が少なくなる
- 「勉強しない生徒」が減る「合格者」が多くなる
という、これまでと逆の組み合わせになるということです。
この場合も因果関係ですが、「増える×増える」という組み合わせを「正の相関」と呼ぶのに対し、上記のような「増える×減る」という組み合わせは「負の相関」と呼びます。以下の記事でも解説しているのでご覧ください。
ループ図:均衡ループ
このような負の相関を持つ因果関係を、ここでは破線(点線)の矢印で表現しています。(※書き方は人によって異なります。プラス・マイナスの記号をつけて書く人もいます。)
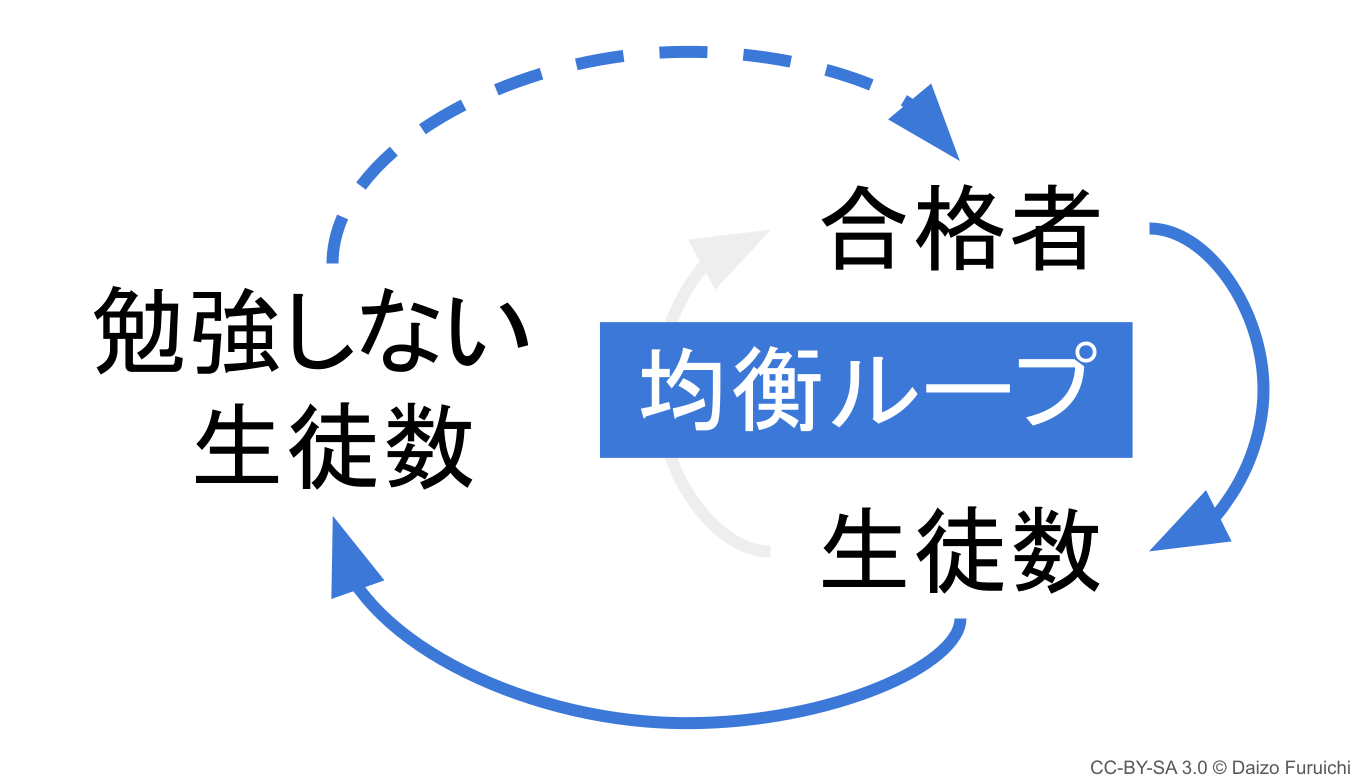
このような、負の相関を持つ矢印(ここでは破線)を奇数個含むループのことを
- 均衡ループ
と呼びます。
ポイントは「奇数個含む」という部分で、上記の例では、実線の矢印2本と、破線の矢印1本(奇数)を含んでいるので「均衡ループ」になります。
この「均衡ループ」とは、名前の通り影響が「均衡する」つまり「バランスを取ろうとする」のが特徴です。
上記の例で言えば、
- 合格者の多さが、一周して合格者の少なさにつながる
という状態、つまり「合格者は多くも少なくもならない」ということになります。